The Weyl Character ring has a basis consisting of the irreducible
representations of 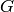 , or equivalently, their characters.
The addition and multiplication in the Weyl character ring
correspond to direct sum and tensor product of representations.
, or equivalently, their characters.
The addition and multiplication in the Weyl character ring
correspond to direct sum and tensor product of representations.
In Sage, many useful features of the Lie group are available as methods of the ambient space:
sage: S=RootSystem("B2").ambient_space(); S
Ambient space of the Root system of type ['B', 2]
sage: S.roots()
[(1, -1), (1, 1), (1, 0), (0, 1), (-1, 1), (-1, -1), (-1, 0), (0, -1)]
sage: S.fundamental_weights()
Finite family {1: (1, 0), 2: (1/2, 1/2)}
sage: S.positive_roots()
[(1, -1), (1, 1), (1, 0), (0, 1)]
sage: S.weyl_group()
Weyl Group of type ['B', 2] (as a matrix group acting on the ambient space)
If you are going to work with representations, you may want to create a Weyl Character ring. Many methods of the ambient space are available as methods of the Weyl Character ring:
sage: B3=WeylCharacterRing("B3")
sage: B3.fundamental_weights()
Finite family {1: (1, 0, 0), 2: (1, 1, 0), 3: (1/2, 1/2, 1/2)}
sage: B3.simple_roots()
Finite family {1: (1, -1, 0), 2: (0, 1, -1), 3: (0, 0, 1)}
sage: B3.dynkin_diagram()
O---O=>=O
1 2 3
B3
Other useful methods of the Weyl character ring include:
Some methods of the ambient space are not implemented as methods of the Weyl Character ring. However the ambient space itself is a method, and so you have access to its methods from the Weyl Character Ring:
sage: B3.space().weyl_group()
Weyl Group of type ['B', 3] (as a matrix group acting on the ambient space)
sage: B3.space()
Ambient space of the Root system of type ['B', 3]
sage: B3.space().rho()
(5/2, 3/2, 1/2)
sage: B3.cartan_type()
['B', 3]
It is useful to give the Weyl Character Ring a name that corresponds to its Cartan Type. This has the effect that the ring can parse its own output:
sage: G2=WeylCharacterRing("G2")
sage: [G2(fw) for fw in G2.fundamental_weights()]
[G2(1,0,-1), G2(2,-1,-1)]
sage: G2(1,0,-1)
G2(1,0,-1)
Actually the prefix for the ring is configurable, so you don’t really have to call this ring G2. Type WeylCharacterRing? at the sage: prompt for details.
There is one important option that you may want to know about. This is coroot notation. You select this by specifying the option style="coroots" when you create the ring. With the coroot style, the fundamental weights are represented (1,0,0, ...), (0,1,0,...) instead of as vectors in the ambient space:
sage: B3 = WeylCharacterRing("B3", style="coroots")
sage: [B3(fw) for fw in B3.fundamental_weights()]
[B3(1,0,0), B3(0,1,0), B3(0,0,1)]
sage: B3(0,0,1)
B3(0,0,1)
sage: B3(0,0,1).degree()
8
The last representation is the eight dimensional spin
representation of 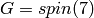 , the double cover of the
orthogonal group
, the double cover of the
orthogonal group 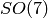 . In the default notation it
would be represented B3(1/2,1/2,1/2).
. In the default notation it
would be represented B3(1/2,1/2,1/2).
With the coroot notation every irreducible representation is represented B3(a,b,c) where a, b and c are nonnegative integers. This is often convenient. For many purposes the coroot style is preferable.
One disadvantage: in the coroot style the Lie group or
Lie algebra is treated as semisimple, so you lose the
distinction between 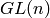 and
and 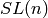 ; you also some
information about representations of E6 and E7 for the
same reason.
; you also some
information about representations of E6 and E7 for the
same reason.
The multiplication in the Weyl Character ring corresponds to tensor product. This gives us a convenient way of decomposing a tensor product into irreducibles:
sage: B3 = WeylCharacterRing("B3")
sage: fw=B3.fundamental_weights()
sage: spinweight = fw[3]; spinweight
(1/2, 1/2, 1/2)
sage: spin = B3(spinweight)
sage: spin.degree()
8
sage: chi = spin*spin; chi
B3(0,0,0) + B3(1,0,0) + B3(1,1,0) + B3(1,1,1)
We have taken the eight-dimensional spin representation and tensored with itself. We see that the tensor square splits into four irreducibles, each with multiplicity one.
The highest weights that appear here are available (with their coefficients) are available through the method hlist:
sage: chi.hlist()
[[(1, 1, 1), 1], [(1, 0, 0), 1], [(1, 1, 0), 1], [(0, 0, 0), 1]]
sage: [p[0] for p in chi.hlist()]
[(1, 1, 1), (1, 0, 0), (1, 1, 0), (0, 0, 0)]
sage: [B3(p[0]) for p in chi.hlist()]
[B3(1,1,1), B3(1,0,0), B3(1,1,0), B3(0,0,0)]
sage: [B3(p[0]).degree() for p in chi.hlist()]
[35, 7, 21, 1]
sage: sum(B3(p[0]).degree() for p in chi.hlist())
64
Here we’ve extracted the individual representations, computed their degrees and checked that they sum to 64.
The weights of the character are (with their coefficients) are available through the method mlist. Continuing from the example in the last section:
sage: chi.mlist()
[[(0, 1, 0), 4], [(1, -1, 1), 1], [(-1, -1, 1), 1],
[(0, 1, 1), 2], [(0, -1, -1), 2], [(0, -1, 0), 4],
[(1, -1, -1), 1], [(0, 1, -1), 2], [(-1, 0, 1), 2],
[(-1, 1, -1), 1], [(-1, -1, 0), 2], [(-1, 1, 0),2],
[(1, 0, 0), 4], [(-1, 0, 0), 4], [(1, 0, -1), 2],
[(0, 0, -1), 4], [(0, -1, 1), 2], [(1, 1, -1), 1],
[(0, 0, 1), 4], [(-1, 0, -1), 2], [(-1, 1, 1), 1],
[(1, 0, 1), 2], [(0, 0, 0), 8], [(-1, -1, -1), 1],
[(1, 1, 1), 1], [(1, 1, 0), 2], [(1, -1, 0), 2]]
The Frobeinus-Schur indicator of an irreducible representation
of a compact Lie group 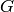 with character
with character 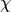 is:
is:
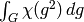
The Haar measure is normalized so that 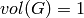 . The Frobenius-Schur
indicator equals 1 if the representation is real (orthogonal),
-1 if it is quaternionic (symplectic) and 0 if it is complex
(not self-contragredient). This is a method of weight ring elements
corresponding to irreducible representations. Let us compute the
Frobenius-Schur indicators of the spin representations of some
odd spin groups:
. The Frobenius-Schur
indicator equals 1 if the representation is real (orthogonal),
-1 if it is quaternionic (symplectic) and 0 if it is complex
(not self-contragredient). This is a method of weight ring elements
corresponding to irreducible representations. Let us compute the
Frobenius-Schur indicators of the spin representations of some
odd spin groups:
sage: for r in [1..4]:
....: R = WeylCharacterRing(['B',r])
....: spinweight = R.fundamental_weights().list()[-1]
....: print r, R(spinweight).frobenius_schur_indicator()
....:
1 -1
2 -1
3 1
4 1
We see that the spin representations of 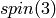 and
and 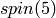 are symplectic, while those of
are symplectic, while those of 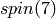 and
and 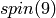 are
orthogonal.
are
orthogonal.
The tensor square of any representation decomposes as the direct sum of the symmetric and exterior squares:
sage: C4=WeylCharacterRing("C4",style="coroots")
sage: chi = C4(1,0,0,0); chi.degree()
8
sage: chi.symmetric_square()
C4(2,0,0,0)
sage: chi.exterior_square()
C4(0,0,0,0) + C4(0,1,0,0)
sage: chi^2 == chi.symmetric_square() + chi.exterior_square()
True
Since in this example the exterior square contains the trivial representation we expect the Frobenius-Schur indicator to be -1, and indeed it is:
sage: chi.frobenius_schur_indicator()
-1
This is not surprising since this is the standard representation of a symplectic group, which is symplectic by definition!
If the representation is truly large you will not be able to construct it in the Weyl character ring, since internally it is represented by a dictionary of its weights. If you want to know its degree, you can still compute that since Sage implements the Weyl dimension formula. The degree of the representation is implemented as a method of its highest weight vector:
sage: L = RootSystem("E8").ambient_space()
sage: [L.weyl_dimension(f) for f in L.fundamental_weights()]
[3875, 147250, 6696000, 6899079264, 146325270, 2450240, 30380, 248]
It is a fact that if 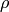 is the Weyl vector then the degree
of the irreducible representation with highest weight
is the Weyl vector then the degree
of the irreducible representation with highest weight 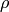 equals
equals 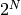 where
where 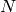 is the number of positive roots. Let
us check this for
is the number of positive roots. Let
us check this for 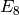 . In this case
. In this case 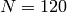 :
:
sage: len(L.positive_roots())
120
sage: 2^120
1329227995784915872903807060280344576
sage: L.weyl_dimension(L.rho())
1329227995784915872903807060280344576
Sage takes the weight space for type ['A',r] to be r+1 dimensional. As a biproduct, if you create the Weyl character ring with the command:
sage: A2=WeylCharacterRing("A2")
Then you are effectively working with GL(3) instead of SL(3). For example, the determinant is the character A2(1,1,1). However, as we will explain later, you can work with SL(3) if you like, so long as you are willing to work with fractional weights. On the other hand if you create the Weyl character ring with the command:
sage: A2=WeylCharacterRing("A2",style="coroots")
Then you are working with SL(3).
There are some advantages to this arrangement.
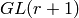 arises frequently in practice. For example, even
if you care mainly about semisimple groups, the group
arises frequently in practice. For example, even
if you care mainly about semisimple groups, the group 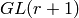 may
arise as a Levi subgroup.
may
arise as a Levi subgroup.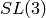 the
fundamental weights are (2/3,-1/3,-1/3) and (1/3,1/3,-2/3). If you
work instead with
the
fundamental weights are (2/3,-1/3,-1/3) and (1/3,1/3,-2/3). If you
work instead with 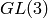 , they are (1,0,0) and (1,1,0). For
many mathematical purposes it doesn’t make any difference which you
use. This is because the difference between (2/3,-1/3,-1/3) and
(1,0,0) is a vector that is orthogonal to all the simple roots. Thus
these vectors are interchangeable. But for convenience avoiding fractional
weights is advantageous.
, they are (1,0,0) and (1,1,0). For
many mathematical purposes it doesn’t make any difference which you
use. This is because the difference between (2/3,-1/3,-1/3) and
(1,0,0) is a vector that is orthogonal to all the simple roots. Thus
these vectors are interchangeable. But for convenience avoiding fractional
weights is advantageous.However if you want to be an SL purist, Sage will support you.
The weight space for SL(3) can be taken to be the hyperplane in
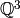 consisting of vectors
consisting of vectors 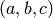 with
with
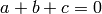 . The fundamental weights for SL(3) are then
(2/3,-1/3,-1/3) and (1/3,1/3,-2/3), though Sage will tell you
they are (1,0,0) and (1,1,0). The work-around is to
filter them through the method coerce_to_sl() as follows:
. The fundamental weights for SL(3) are then
(2/3,-1/3,-1/3) and (1/3,1/3,-2/3), though Sage will tell you
they are (1,0,0) and (1,1,0). The work-around is to
filter them through the method coerce_to_sl() as follows:
sage: A2=WeylCharacterRing("A2")
sage: [fw1,fw2]=[A2.coerce_to_sl(w) for w in A2.fundamental_weights()]
sage: [standard, contragredient] = [A2(fw1), A2(fw2)]
sage: standard, contragredient
(A2(2/3,-1/3,-1/3), A2(1/3,1/3,-2/3))
sage: standard*contragredient
A2(0,0,0) + A2(1,0,-1)
Sage is not confused by the fractional weights. Note that if you use coroot notation, you are working with SL automatically:
sage: A2=WeylCharacterRing("A2",style="coroots")
sage: A2(1,0).mlist()
[[(2/3, -1/3, -1/3), 1], [(-1/3, 2/3, -1/3), 1], [(-1/3, -1/3, 2/3), 1]]
There is no convenient way to create the determinant in the Weyl Character Ring if you adopt the coroot style.
Just as we coerced the fundamental weights into the 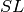 weight
lattice, you may need to coerce the Weyl vector
weight
lattice, you may need to coerce the Weyl vector 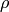 if you are
working with
if you are
working with 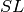 . The default value for
. The default value for 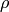 in type
in type
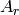 is
is 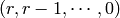 ,
but if you are an SL purist you want
,
but if you are an SL purist you want
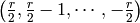 .
Therefore take the value of rho that you get from the method of the
ambient space and coerce it into SL:
.
Therefore take the value of rho that you get from the method of the
ambient space and coerce it into SL:
sage: rho = A2.coerce_to_sl(A2.space().rho()); rho
(1, 0, -1)
sage: rho == (1/2)*sum(a for a in A2.space().positive_roots())
True
You do not need to do this for other Cartan types. If you are working with (say) F4 then a rho is a rho is a rho:
sage: F4 = WeylCharacterRing("F4")
sage: L = F4.space()
sage: rho = L.rho()
sage: rho == (1/2)*sum(a for a in L.positive_roots())
True
You may improve the performance of a Weyl character ring by specifying cache=True when you create the ring. This means that the results of intermediate computations are saved. The amount of improvement would depend on the type of computation you are doing.