Generators and Relations
Our explanation of universal properties in Section 1.2 was not adequate, due to the fact that we had not sufficiently developed categorical language. We will remedy this now with a fuller explanation.
A category $\mathcal{C}$ consists of a class whose elements are called objects of the category, and for every pair $A, B \in \mathcal{C}$ of objects there is a set $\operatorname{Hom} (A, B) = \operatorname{Hom}_{\mathcal{C}} (A, B)$ whose elements are called morphisms. It is assumed that if $f \in \operatorname{Hom} (A, B)$ and $g \in \operatorname{Hom} (B, C)$, then there is a composite morphism $g \circ f \in \operatorname{Hom} (A, C)$. It is assumed that if (furthermore) $h \in \operatorname{Hom} (C, D)$ then we have $h \circ (g \circ f) = (h \circ g) \circ f$ in $\operatorname{Hom} (A, D)$. Furthermore, there is a special element $1_A \in \operatorname{Hom} (A, A)$ such that if $f \in \operatorname{Hom} (A, B)$ then $f \circ 1_A = 1_B \circ f = f$.
For reasons explained in Section 1.2 the objects are not assumed to form a set. However if $A$ and $B$ are objects, $\operatorname{Hom} (A, B)$ is a set.
The first examples of categories that one encounters are familiar algebraic objects. There is the category of sets, in which the morphisms are maps, the category of groups, in which the morphisms are homomorphisms, and so forth. There is the category of topological spaces, in which the morphisms are continuous maps. There is the category of modules over a fixed ring $R$, and if $R =\mathbb{Z}$, this reduces to the category of abelian groups. There is the category of rings, with ring homomorphisms. And so on.
All of the above examples are sets with additional structure, but we will encounter other categories in which the objects are not sets at all.
If $\mathcal{C}$ and $\mathcal{D}$ are categories, a functor from $\mathcal{C}$ to $\mathcal{D}$ is a construction which, for every object $A \in \mathcal{C}$ produces an object $\mathcal{F}A \in \mathcal{D}$. It is assumed that there is also a map \[ \operatorname{Hom} (A, B) \mathop{\longrightarrow}\limits^{\mathcal{F}} \operatorname{Hom} (\mathcal{F}A, \mathcal{F}B) \] such that $\mathcal{F}(g \circ f) =\mathcal{F}g \circ \mathcal{F}f$ if $f \in \operatorname{Hom} (A, B)$ and $g \in \operatorname{Hom} (B, C)$. In other words, the functor respects composition.
Functors are ubiquitous. As a first example, we will develop a functor from the category of sets to the category of groups, called the free group. It will be characterized by a universal property.
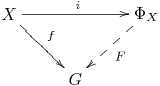
Theorem 1.8.1: If $X$ is a set, there is a group $\Phi_X$ with a map $i : X \longrightarrow \Phi_X$ such that if $f : X \longrightarrow G$ is any map from $X$ into a group $G$, then there is a unique group homomorphism $F : \Phi_X \longrightarrow G$ such that $f = f \circ i$. The map $i$ is injective.
The property that $\Phi_X$ is asserted to have is called the universal property of the free group. The last assertion that $i$ is injective is not part of the universal property, but a useful fact that allows us to identify $X$ with $i (X) \subset \Phi_X$. The universal property is summarized by the following commutative diagram:
|
Proof. (Click to Expand/Collapse)
We define an equivalence relation on $\Sigma$, namely, two words are equivalent if one can be obtained from the other by inserting and removing pairs of the form $x x^{- 1}$ or $x^{- 1} x$ with $x \in X$. Thus if $X =\{a, b, c\}$ the words $a b b^{- 1} a c$ and $a a a^{- 1} a c b^{- 1} b$ are equivalent. We define $\Phi_X$ to be the set of equivalence classes of $\Sigma$ modulo this equivalence relation.
We can multiply words by concatenation: $w_1 \cdots w_n \cdot v_1 \cdots v_m = w_1 \cdots w_m v_1 \cdots v_m$. This multiplication is obviously compatible with equivalence in that if $\alpha, \alpha', \beta, \beta' \in \Sigma$ with $\alpha \sim \alpha'$ and $\beta \sim \beta'$ then $\alpha \cdot \beta \sim \alpha' \cdot \beta'$. So there is induced a multiplication on $\Phi_X$, which becomes a group. The class of the empty word is the identity element, and to define the inverse of a word $w_1 w_2 \cdots w_n$ we just write the elements in reverse order and replace $x \in X$ by $x^{- 1}$ when it appears, and $x^{- 1}$ by $x$.
Now to verify the universal property. The map $i : X \longrightarrow \Phi_X$ sends $x \in X$ to the equivalence class of the word $x$ of length 1 in $\Sigma$. This map is injective, and we will identify $X$ with its image in $\Phi_X$.
Suppose that $f : X \longrightarrow G$ is any map, where $G$ is a group. We define $f (x^{- 1}) = f (x)^{- 1}$ for $x \in X$, and then if $w_1 \cdots w_n$ is any word, we can define $F (w_1 \cdots w_n) = f (w_1) \cdots f (w_n)$. To see that this is well defined, if another word $v_1 \cdots v_m$ is equivalent to $w_1 \cdots w_n$ it can be obtained from $w_1 \cdots w_n$ by inserting and deleting pairs $x x^{- 1}$ or $x^{- 1} x$ with $x \in X$. We can perform these operations in parallel in $G$; wherever $x x^{- 1}$ or $x^{- 1} x$ is inserted or deleted in $\Sigma$ we insert or delete $f (x) f (x^{- 1})$ or $f (x^{- 1}) f (x)$ in $G$, and this does not change the value of $f (w_1) \cdots f (w_n)$ because $G$ is a group, and $f (x) f (x^{- 1}) = f (x) f (x)^{- 1} = 1$ and similarly $f (x^{- 1}) f (x) = 1$. Thus $f (w_1) \cdots f (w_n) = f (v_1) \cdots f (v_n)$ and we see that the map $F$ is well-defined.
Since the multiplication in $\Phi_X$ is just concatenation it is obvious that $F$ is a group homomorphism. Moreover, the homomorphism $F$ is unique, because the condition $F \circ i = f$ means that $F (x) = f (i (x)) = f (x)$ when $x \in X$, and similarly (since $F$ is a homomorphism) $F (x^{- 1}) = F (x^{- 1}) = f (x)^{- 1}$. Thus $F (w_1 \cdots w_n) = f (w_1) \cdots f (w_n)$; we see that the homomorphism $F : \Phi_X \longrightarrow G$ is uniquely determined.
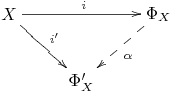
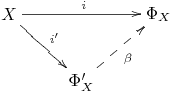
Proposition 1.8.1: The free group $\Phi_X$ is determined up to isomorphism by its universal property. More formally, let $i' : X \longrightarrow \Phi'_X$ be another map of $X$ into a group, and assume that whenever $f : X \longrightarrow G$ is a map from $X$ into a group, there is a unique group homomorphism $F' : \Phi_X' \longrightarrow G$ such that $f = F' \circ i'$. Then there is an isomorphism $\alpha : \Phi_X \longrightarrow \Phi'_X$ such that $i' = \alpha \circ i$.
Proof. (Click to Expand/Collapse)
|
|
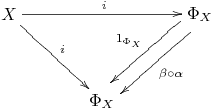
To show that $\alpha$ is an isomorphism, we will argue that $\alpha$ and $\beta$ are inverse maps, in other words, $\beta \circ \alpha = 1_{\Phi_X}$ and $\alpha \circ \beta = 1_{\Phi'_X}$. To see this, we observe that there are two different homomorphisms $\Phi_X \longrightarrow \Phi_X$ that we want to compare, namely $\beta \circ \alpha$ and $1_{\Phi_X}$. To show that they are the same we will invoke the uniqueness assertion in the universal property. Indeed, either of the two maps $\beta \circ \alpha$ or $1_{\Phi_X}$ makes the following diagram commute:
|
Now let us explain another way of thinking about this. We will say that an object $I$ in a category is an initial object if $\operatorname{Hom} (I, A)$ has exactly one element for all objects $A$. Thus in the category of sets, the empty set is an initial object. Similarly, we will say that an object $T$ in a category is an terminal object if $\operatorname{Hom} (A, T)$ has exactly one element for all objects $A$.
Exercise 1.8.1: The category of sets has both an initial object and a terminal object. What are they?
Exercise 1.8.2: The category of groups has both an initial object and a terminal object. What are they?
The notion of an isomorphism makes sense in an arbitrary category. Indeed, we say two objects $X$ and $Y$ are isomorphic if there are morphisms $f : X \longrightarrow Y$ and $g : Y \longrightarrow X$ such that $g \circ f = 1_X$ and $f \circ g = 1_Y$, and in this case we call $f$ and $g$ inverse isomorphisms.
Proposition 1.8.2: Any two initial objects in a category are isomorphic, and any two terminal objects are isomorphic.
Proof. (Click to Expand/Collapse)
We note that the proof of Proposition 1.8.2 is formally very similar to the proof of Proposition 1.8.1, and indeed, we can deduce Proposition 1.8.1 from Proposition 1.8.2. At the same time, we will keep an earlier promise, and give an example of a category whose objects are not sets with additional structure, but something slightly more subtle.
We introduce an auxiliary category $\mathcal{C}_X$. With the set $X$ fixed, the objects in $\mathcal{C}_X$ consist of all maps of $X$ into groups. More formally, an object in $\mathcal{C}$ is a pair $\Gamma = (G, f)$, where $G$ is a group and $f : X \longrightarrow G$ a map. Note that the group structure on $G$ is irrelevant for defining the objects, but it becomes important for defining the morphisms. If $\Gamma' = (G', f')$ is another object, $\operatorname{Hom} (\Gamma, \Gamma')$ consists of the set of all group homomorphisms $\phi : G \longrightarrow G'$ such that the following diagram commutes:
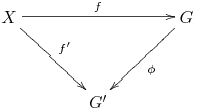
|
With these definitions in place, we see that the free group $\Phi_X$ is just an initial object in the category $\mathcal{C_X$}.
A universal property is a propery like this one that can be expressed as saying that something is an initial or terminal object in an appropriate category.
Exercise 1.8.3: Formulate a category that allows you recognize the universal property of the product as the assertion that some object is terminal. (See Proposition 1.3.4.)
Exercise 1.8.4: Formulate a category that allows you to recognize the universal property of the field of fractions of an integral domain as the assertion that some object is initial. (See Exercise 1.2.6.)
An object characterized by a universal property generally gives rise to a functor. Le us see this in the case of the free group. For every set $X$ we choose a free group and an embedding $i_X : X \longrightarrow \Phi_X$. It can be the explicit one described in the proof of Theorem 1.8.1, but it doesn't have to be – the object $\Phi_X$ is unique up to isomorphism, and for each set $X$ we pick a $\Phi_X$.
If $f : X \longrightarrow Y$ is some map in the category of sets, then we have a map $i_Y \circ f : X \longrightarrow \Phi_Y$ and using the universal property of $\Phi_X$ there is then a unique group homomorphism $\mathcal{F}f : \Phi_X \longrightarrow \Phi_Y$ such that the following diagram commutes:
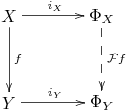
|
Exercise 1.8.5: Prove that $\mathcal{F}$ is a functor.
Lastly, let us show that the notion of a free group allows us to make the notion of a presentation rigorous. We consider the group with these generators and relations: \[ G = \left\langle x, y| x^7 = y^3 = 1, y x y^{- 1} = x^2 \right\rangle . \] What this really means is that $G$ is a group with the given generators and relations, and none that cannot be deduced from them. But the last clause is vague. To give a rigorous characterization, we ask that $G$ have the following property.
- For any group $H$ with generators $\xi$ and $\eta$ that satisfy the same relations, that is \begin{equation} \xi^7 = \eta^3 = 1, \hspace{2em} \eta \xi \eta^{- 1} = \xi^2 \end{equation} there is a unique group homomorphism $f : G \longrightarrow H$ with $f (x) = \xi$ and $f (y) = \eta$.
To see that such a group exists, let $\Phi_X$ be the free group on $X =\{\mathbf{x}, \mathbf{y}\}$. (We are using a bold font to distinguish between $x$ and $\mathbf{x}$, but we've chosen one element in $X$ for each given generator.) Let $N$ be the smallest normal subgroup that contains $\mathbf{x}^7$, $\mathbf{y}^3$ and $\mathbf{y}\mathbf{x}\mathbf{y}^{- 1} \mathbf{x}^{- 3}$.
Exercise 1.8.6: Explain why there is a smallest normal subgroup containing $\mathbf{x}^7$, $\mathbf{y}^3$ and $\mathbf{y}\mathbf{x}\mathbf{y}^{- 1} \mathbf{x}^{- 3}$.
We define $G$ to be $\Phi_X / N$. Let $x$ and $y$ be the images of $\mathbf{x}$ and $\mathbf{y}$ in this quotient.
Proposition 1.8.3: The group $G$ has the advertised universal property.
Proof. (Click to Expand/Collapse)