Semidirect Products
In this Section, we will look at the notation of a direct product, first for general groups, then more specifically for abelian groups and for rings; and we will consider a related, more general notion, called the semidirect product.
If $G$ and $H$ are groups, we may form the group $G \times H$, which is the Cartesian product. As a set, it is the set of ordered pairs $(g, h)$ such that $g \in G$ and $h \in H$. As a group, its multiplication is given by \[ (g, h) \cdot (g', h') = (g g', h h') . \] Its cardinality is obviously $|G| \cdot |H|$. We will sometimes refer to $G \times H$ as the external direct product for reasons that will become clear momentarily. We point out that it has two natural subgroups $G \times 1 =\{(g, 1) |g \in G\}$ and $1 \times H =\{(1, h) | h \in H\}$. We have $G \cong G \times 1$ since $g \longmapsto (g, 1)$ is an isomorphism $G \longrightarrow G \times 1$ and similarly $H \cong 1 \times H$. So we think of $G \times H$ as a group containing a copy of $G$ (that is, a subgroup isomorphic to $G$) and a copy of $H$. These copies commute, that is, if $x \in G \times 1$ and $y \in 1 \times H$ then we have $x y = y x$.
We ask the question, given a group $P$ containing a copy of $G$ and a copy of $H$, under what circumstances can we conclude that $P \cong G \times H$?
Proposition 1.3.1: Let $G$ and $H$ be normal subgroups of $P$. Assume that $G \cap H = 1$ and that $G H = P$. Then $P \cong G \times H$. More precisely, the subgroups $G$ and $H$ commute with each other, and the multiplication map $G \times H \longrightarrow P$ is a group isomorphism.
Here, as always, $1$ denotes the trivial subgroup $\{1\}$ of $P$.
Proof. (Click to Expand/Collapse)
We have proved that $G$ and $H$ commute. Now consider the map $\mu : G \times H \longrightarrow P$ given by multiplication: $\mu (g, h) = g h$. It follows easily from the commutativity of $G$ and $H$ that this is a homomorphism. It is surjective since $G H = P$, and it is injective since $G \cap H = 1$; indeed if $(g, h)$ is in the kernel then $g = h^{- 1}$ is in $G \cap H$ so $g = h = 1$.
We refer to $P$ as the internal direct product of $G$ and $H$ if $G$ and $H$ are subgroups satisfying the hypotheses of Proposition 1.3.1.
Example 1.3.1: Let $P$ be a cyclic group of order 6; specifically, let $P = \left\langle x \right\rangle$ where $x^6 = 1$. Then $P$ has two subgroups of orders $2$ and $3$: \[ G = \left\langle x^3 \right\rangle =\{1, x^3 \}, \] \[ H = \left\langle x^2 \right\rangle = \left\{ 1, x^2, x^4 \right\} . \] It is clear that $G \cap H = 1$, and easy to verify that $G H = P$. Thus $P$ is the internal direct product of $G$ and $H$.
Now an external direct product is an internal direct product, since if $P = G \times H$ then as we have already explained, $P$ contains subgroups $G \times 1$ and $1 \times H$ isomorphic to $G$ and $H$ respectively, and $P$ is the internal direct product of these. We see that internal and external direct products are equivalent, and the only real difference between them is how they are viewed, or come up in practice.
Remark 1.3.1: There is a common abuse of language that is useful from a psychological point of view, which is to identify two groups (or rings, fields ...) that are isomorphic. In other words, we pretend that the two groups are the same, since no confusion can result, only clarification. Thus if $P = G \times H$ is the external direct product of $G$ and $H$, the subgroups $G \times 1$ and $1 \times H$ are isomorphic to $G$ and $H$, and we may identify $G \times 1$ and $1 \times H$ with $G$ and $H$, respectively. Then we see that $P$ is the internal direct product of $G$ and $H$, as well as the external.
Exercise 1.3.1: To illustrate the application of this convenient abuse of language, we may summarize Exercise 1.2.7 by saying that "the field of fractions is the smallest field containing the integral domain $R$.'' Explain this point.
We have not yet defined the internal direct product of more than two groups. Let us do so now. If $H_1, \cdots, H_r$ are subgroups of $G$, we say $G$ is the internal direct product of $H_1, \cdots, H_r$ if $H_i$ and $H_j$ commute when $i \neq j$, and if every element of $G$ can be written uniquely in the form $h_1 \cdots h_r$ with $h_i \in H_i$.
We can weaken the definition of a direct product slightly. We say that the group $P$ is the (internal) semidirect product of $G$ and $H$ if one of them is normal, $G H = P$ and $G \cap H =\{1\}$. Let us say for definiteness that $G \trianglelefteq P$. In this case we write $P = G \rtimes H$ or $P = H \ltimes G$. (The notation is asymmetrical, so a useful thing to remember is that in any one of the symbols $\vartriangleleft$, $\ltimes$ or $\rtimes$ the triangle points to the normal subgroup.)
We now introduce the language of short exact sequences. Exact sequences are especially important in homological algebra, which is a fundamental tool in certain areas such as algebraic topology. Outside of homological algebra, they are still culturally important, since it is often handy to say something like this:
If \[ 1 \longrightarrow G' \longrightarrow G \longrightarrow G'' \longrightarrow 1 \] is a short exact sequence, then $G$ has Property $X$ if and only if both $G'$ and $G''$ have Property X. |
If we have two homomorphisms involving three groups \[ K \mathop{\longrightarrow}\limits^f G \mathop{\longrightarrow}\limits^g H \] we call this sequence exact at $G$ if $\operatorname{im} (f) = \ker (g)$. Note that both $\operatorname{im} (f)$ and $\ker (g)$ are subgroups of $G$, so this statement makes sense. The notation $K \mathop{\longrightarrow}\limits^f G$ is another way of writing $f : K \longrightarrow G$, and since we are working in the category of groups, it is understood that $f$ is a homomorphism.
Exercise 1.3.2: (a) Prove that $1 \longrightarrow G \mathop{\longrightarrow}\limits^g H$ is exact if and only if $g$ is injective. Here $1$ denotes the group $\{1\}$ with just one element, and we don't have to specify the homomorphism $1 \longrightarrow G$ because there is only one.
(b) Prove that $K \mathop{\longrightarrow}\limits^f G \longrightarrow 1$ is exact if and only if $f$ is surjective.
(c) Prove that if $K \mathop{\longrightarrow}\limits^f G \mathop{\longrightarrow}\limits^g H$ is exact then $g \circ f$ is the trivial homomorphism that maps everything in $K$ to $1 \in H$.
Now suppose that we have a sequence:
| \[ 1 \longrightarrow K \mathop{\longrightarrow}\limits^f G \mathop{\longrightarrow}\limits^g Q \longrightarrow 1 \] | (1.3.1) |
If we have a diagram with different arrows representing homomorphisms, such as this square: \[ \begin{array}{llllllll} 1 & \longrightarrow & K & \mathop{\longrightarrow}\limits^f & G & \mathop{\longrightarrow}\limits^g & Q & \longrightarrow 1\\ & & \downarrow \scriptsize{\kappa} & & \downarrow \scriptsize{\gamma} & & \downarrow \scriptsize{\eta} & \\ 1 & \longrightarrow & K' & \mathop{\longrightarrow}\limits^{f'} & G' & \mathop{\longrightarrow}\limits^{g'} & Q' & \longrightarrow 1 \end{array} \] we say that the diagram is commutative if whenever there are two ways of getting from one group to the other, they give the same result. Thus in this diagram, there are two compositions that go from $K$ to $G'$, namely $\gamma \circ f$ and $f' \circ \kappa$, so saying the diagram is commutative means that $\gamma f = f' \kappa$, and similarly $\eta g = g' \gamma$.
Proposition 1.3.2:
Suppose that (1.3.1) is a short exact sequence. Then $K$ is
isomorphic to a normal subgroup $G'$ of $G$, and $Q$ is isomorphic to $G /
G'$. We have a commutative diagram, where the rows are exact and the
vertical arrows are isomorphisms (in fact the identity map for the middle
arrow $G \longrightarrow G$).
Here $i : G' \longrightarrow G$ is the inclusion map and $\pi : G
\longrightarrow G / G'$ the projection.
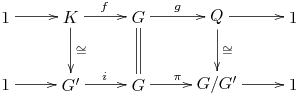
The existence of these three isomorphisms is enough to make the two short exact sequences \[1 \longrightarrow K \longrightarrow G \longrightarrow Q \longrightarrow 1\] and \[1 \longrightarrow G' \longrightarrow G \longrightarrow G / G' \longrightarrow 1\] equivalent for most purposes. Thus in the spirit of Remark 1.3.1 that when we are presented with the short exact sequence (1.3.1) there is no loss of generality in pretending that $K$ is a normal subgroup of $G$ and $Q$ is the quotient group $G / K$.
Proof. (Click to Expand/Collapse)
Short exact sequences give a convenient way of talking about direct and semidirect products.
Proposition 1.3.3: Let $1 \longrightarrow K \mathop{\longrightarrow}\limits^f G \mathop{\longrightarrow}\limits^g Q \longrightarrow 1$ be a short exact sequence. Suppose that there exists a homomorphism $s : Q \longrightarrow G$ such that $g \circ s = 1_Q$. Then \[ G = \operatorname{im} (f) \rtimes \operatorname{im} (s) . \]
This situation is often represented thus:
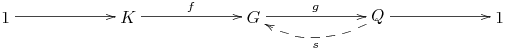
|
Proof. (Click to Expand/Collapse)
We show that $\operatorname{im} (f) \cdot \operatorname{im} (s) = G$. First, if $x \in G$, write $x = y \cdot z$ where $z = s g (x)$ and $y = x z^{- 1}$. We have $g (z) = g s g (x) = 1_Q (g (x)) = g (x)$, and so $g (y) = g (x) g (z)^{- 1} = 1$. Thus $y \in \ker (g) = \operatorname{im} (f)$. On the other hand $z \in \operatorname{im} (s)$ by construction, so $\operatorname{im} (f) \cdot \operatorname{im} (s) = G$.
Finally, we show that $\operatorname{im} (f) \cap \operatorname{im} (s) = 1$. Suppose that $x \in \operatorname{im} (f) \cap \operatorname{im} (s)$. Then we can write $x = f (k) = s (q)$ where $k \in K$ and $q \in Q$. Then $q = 1_Q (q) = g s (q) = g f (k) = 1$ since $g \circ f$ is the trivial homomorphism mapping all $K$ to the $1 \in Q$ (Exercise 1.3.2).
It is now clear that $G$ is the semidirect product.
If $s : Q \longrightarrow G$ exists as in Proposition 1.3.3 it is called a splitting, and we say that the short exact sequence is split. Thus in the context of groups, a split short exact sequence is essentially equivalent to a semidirect product. Exercise 1.3.4 shows that not every short exact sequence is split.
Exercise 1.3.3: Show that the cyclic group $Z_n$ of order $n$ has a unique subgroup of order $d$ for every divisor $d$ of $n$, and that this subgroup is cyclic.
Exercise 1.3.4: Show that there is a short exact sequence \[ 1 \longrightarrow Z_n \longrightarrow Z_{n m} \longrightarrow Z_m \longrightarrow 1, \] and that this short exact sequence is split if and only if $n$ and $m$ are coprime.
Exercise 1.3.5:
Let there be given a short exact sequence
\[
1 \longrightarrow K \longrightarrow G
\mathop{\longrightarrow}\limits^{\pi} Q \longrightarrow 1.
\]
(1.3.2)
| \[ 1 \longrightarrow K \longrightarrow G_1 \mathop{\longrightarrow}\limits^{\pi} Q_1 \longrightarrow 1, \hspace{2em} 1 \longrightarrow K \longrightarrow G_2 \mathop{\longrightarrow}\limits^{\pi} Q_2 \longrightarrow 1, \] | (1.3.3) |
For the rest of this section, we will look more closely at abelian groups, which we will write additively. The natural generalization of this discussion is to modules over a ring. Although we will not work in such generality, rings will play an important role in this discussion.
We first note that for an abelian group, any subgroup is automatically normal, so there is no distinction between the direct product and the semidirect product.
The fact that abelian groups are modules over $\mathbb{Z}$ is important because $\mathbb{Z}$ is a principal ideal domain. Most of the basic theory of abelian groups can be generalized (usefully) to modules over principal ideal domains. We won't strive for such generality here, however. We will content ourselves with developing a few properties of the direct product in the generality of a module over an arbitrary ring, and when the ring later needs to be a principal ideal domain, we will just take it to be $\mathbb{Z}$.
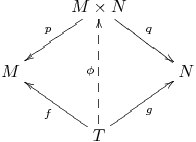
Proposition 1.3.4: Let $M$ and $N$ be (left) modules over a ring $R$.
(a) There exist homomorphisms $p : M \times N \longrightarrow M$ and $q : M \times N \longrightarrow N$ such that if $T$ is any $R$-module and $f : T \longrightarrow M$ and $g : T \longrightarrow N$ are homomorphisms, then there exists a unique homomorphism $\phi : T \longrightarrow M \times N$ such that $f = p \circ \phi$ and $g = q \circ \phi$.
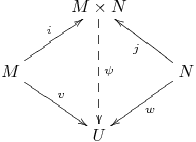
(b) There exist homomorphisms $i : M \longrightarrow M \times N$ and $j : N \longrightarrow M \times N$ such that if $U$ is any $R$-module and $v : M \longrightarrow U$ and $w : N \longrightarrow U$ are homomorphisms then there exists a unique homomorphism $\psi : M \times N \longrightarrow U$ such that $v = \psi \circ i$ and $w = \psi \circ j$.
These properties can be expressed quickly by means of commutative diagrams.
|
|
Proof. (Click to Expand/Collapse)
Property (a) is called the "universal property of the product,'' and property (b) is called the "universal property of the coproduct.'' The proper context for considering them in their full generality is category theory, which we will not develop, but we do offer a few remarks. Mathematical objects are organized into categories, such as the category of groups, the category of sets, the category of topological spaces, the category of modules over a fixed ring $R$, etc. Within each category, the maps are as important as the objects themselves; for the categories just mentioned, these are, respectively, all maps, all continuous maps, and all $R$-module homomorphisms. Although we will not develop category theory, we will not hesitate to call the reader's attention to categorical ideas in an informal way.
In any category, there may or may not be a product of two objects, and there may or may not be a coproduct. If there is a product and there is a coproduct, the two may or may not be the same, as the following exercise shows.
Exercise 1.3.6: Let $X$ and $Y$ be sets. (a) Show that if $X \times Y$ is the Cartesian product of $X$ and $Y$, show that the universal property of the product is satisfied: that is, if $p : X \times Y \longrightarrow X$ and $q : X \times Y \longrightarrow Y$ are the projection maps, defined by $p (x, y) = x$ and $q (x, y) = y$, and if $T$ is any set and $f : T \longrightarrow X$ and $g : T \longrightarrow Y$ are any maps, then there exists a unique map $\phi : T \longrightarrow X \times Y$ such that $f = p \circ \phi$ and $g = q \circ \phi$.
(b) Describe a set $Z$ with maps $i : X \longrightarrow Z$ and $j : Y \longrightarrow Z$ that satisfies the universal property of the coproduct, and observe that in this category, the product and coproduct are not the same.
Remark 1.3.2: The last exercise shows that it is remarkable that in the category of modules over a ring, the product and coproduct of two modules produce the same object. If $M$ and $N$ are modules over a ring (for example Abelian groups, if that ring is $\mathbb{Z}$), both notations $M \times N$ and $M \oplus N$ are used to denote the same object. Generally we will use the notation $M \oplus N$ for modules over a ring, and in particular for abelian groups (which are $\mathbb{Z}$-modules) if they are written additively. We will use the notation $G \times H$ for groups, including abelian groups, if they are written multiplicatively. The notation $M \times N$ does not have to be absolutely avoided for abelian groups or modules; this notation would be used in a context where the universal property of the product is more relevant, and the notation $M \oplus N$ would be used in a context where the universal property of the coproduct is more relevant. We note that $G \times H$ is not the coproduct in the category of groups. (Instead, there is a "free product.'') And $R \times S$ is not the coproduct in the category of rings. (Instead, there is a "tensor product.'') See Remark 1.3.3.
Exercise 1.3.7: Show that if $R$ and $S$ are rings, then $(R \times S)^{\times} = R^{\times} \times S^{\times}$.
Next, we define the endomorphism ring of an abelian group. Let $G$ be an abelian group, written additively. Then we define the endomorphism ring $\operatorname{End} (G)$ to be the ring of endomorphisms, which are by definition homomorphisms $G \longrightarrow G$. The additive structure of the ring $\operatorname{End} (G)$ is by addition of functions, while the multiplication is composition. Thus \[ (\phi + \psi) (x) = \phi (x) + \psi (x), \hspace{2em} (\phi \psi) (x) = \phi (\psi (x)) . \]
Exercise 1.3.8: Convince yourself that $\operatorname{End} (G)$ is a ring.
Exercise 1.3.9: Explain why $G$ is a module over $\operatorname{End} (G)$.
Let $R$ be a ring. By the center $Z (R)$ we mean the subring of elements that commute with the whole ring. Thus \[ Z (R) =\{z \in R| \text{$z r = r z$ for all $r \in R$\}} . \]
Proposition 1.3.5: (i) If $A$ is an abelian group, written additively, and if $a \in A$, there is a unique group homomorphism $f : \mathbb{Z} \longrightarrow A$ such that $f (1) = a$.
(ii) If $R$ is a ring then there is a unique ring homomorphism $f : \mathbb{Z} \longrightarrow R$. We have $f (\mathbb{Z}) \subseteq Z (R)$.
Proof. (Click to Expand/Collapse)
To prove (ii), we choose the $\mathbb{Z}$-module homomorphism constructed in (i) such that $f (1) = 1$. To see that it is a ring homomorphism, it must be checked that $f (m n) = f (m) f (n)$. A ring homomorphism must by definition satisfy $f (1) = 1$, so if such a ring homomorphism exists it is this map. We leave it to the reader to check that this is a ring homomorphism. Since $1 \in Z (R)$, and since the image of $f$ consists of multiples of $1$, the image $f (\mathbb{Z})$ is contained in $Z (R)$.
Now we discuss the notion of the direct product of rings; eventually we will want to use these ideas to study group algebras.
If $R, S$ are rings, we can form the external direct product $R \times S$, which now has both an additive structure and a multiplicative one: \[ (r, s) + (r', s') = (r + r', s + s'), \hspace{2em} (r, s) (r', s') = (r r', s s') . \] It is a ring with unit $1_{R \times S} = (1, 1)$. There are ring homomorphisms
| \[ R \mathop{\longleftarrow}\limits^p R \times S \mathop{\longrightarrow}\limits^q S, \hspace{2em} p (r, s) = r, \hspace{1em} q (r, s) = s, \] | (1.3.4) |
Is there a corresponding notion of an internal direct product of rings? We will answer this question affirmatively soon after some preliminary discussion. If $T$ is a ring and $e \in T$, then $e$ is called an idempotent if $e^2 = e$. It is called central if it lies in the center of $T$. And, two idempotents $e$ and $f$ are called orthogonal if $e f = f e = 0$. If they are orthogonal, then $e + f$ is also an idempotent.
For example, \[ e = (1, 0), \hspace{2em} f = (0, 1) \] are idempotents in $R \times S$. We way they are central since $e, f \in Z (R \times S)$. Finally, we say they are orthogonal since $e f = f e = 0$.
Remark 1.3.3: In addition to the ring homomorphisms (1.3.4), one might think that there are also ring homomorphisms \[ R \mathop{\longrightarrow}\limits^i R \times S \mathop{\longleftarrow}\limits^j S, \hspace{2em} i (r) = (r, 0), \hspace{1em} j (s) = (0, s) . \] Indeed, these maps satisfy most of the requirements of a ring homomorphism $i (r + r') = i (r) + i (r')$, $i (r r') = i (r) i (r')$. But they are not ring homomorphisms because $i (1) = (1, 0) \neq 1_{R \times S}$ and $j (1) = (0, 1) \neq 1_{R \times S}$. For the same reason, $i (R)$ and $i (S)$ are not considered subrings of $R \times S$. They are two-sided ideals. In keeping with Remark 1.3.1, we may identify $R$ and $S$ with $i (R)$ and $j (S)$, respectively, but in doing so we must remember that they are not subrings, even though they are rings and have identity elements.
We may now describe "internal'' direct products of rings. The basic data needed to do this is to exhibit a pair of central orthogonal idempotents.
Proposition 1.3.6: Let $T$ be a ring. Suppose $1 = e + f$ where $e$ and $f$ are central orthogonal idempotents. Let $R = e T$ and $S = f T$. Then $R$ and $S$ are two-sided ideals. Moreover $R$ is a ring with unit $e$ and $S$ is a ring with unit $f$. The ring $T$ is isomorphic to the direct product $R \times S$.
Proof. (Click to Expand/Collapse)
Next let us check that $T$ is the internal direct sum of $R$ and $S$ as an abelian group. Thus we need to check that $R + S = T$ and $R \cap S =\{0\}$. If $t \in T$ we can write \[ t = 1 \cdot t = e \cdot t + f \cdot t \in R + S, \] so $R + S = T$. If $x \in R \cap S$ we can write $x = e t = f t'$. Then \[ x = 1 \cdot x = e \cdot x + f \cdot x = e f t' + f e t = 0 + 0 = 0 \] so $R \cap S =\{0\}$.
Now the abelian group isomorphism $T \cong R \times S$ that was constructed in Proposition 1.3.1 is easily seen to be compatible with multiplication, and $1 \in T$ corresponds to $(e, f) \in R \times S$, that is, $(1_R, 1_S)$ since $e = 1_R$ and $f = 1_S$ are the units in these rings. So this abelian group isomorphism is an isomorphism of rings.
As an illustration, let us use idempotents to prove the Chinese Remainder Theorem.
Proposition 1.3.7: (Chinese Remainder Theorem)Assume that $m$ and $n$ are coprime. Then \[ \mathbb{Z}/ m n\mathbb{Z} \cong (\mathbb{Z}/ m\mathbb{Z}) \times (\mathbb{Z}/ n\mathbb{Z}) \] as rings.
Proof. (Click to Expand/Collapse)
We have a commutative diagram

|
The following exercise gives another way that idempotents are connected with direct product decompositions.
Exercise 1.3.10: Let $G$ be an abelian group, and let $\phi \in \operatorname{End} (E)$. Suppose that $\phi$ is an idempotent, that is, $\phi^2 = \phi$. Prove that $G = \ker (\phi) \oplus \operatorname{im} (\phi)$.
Our goal is the structure theory for finite abelian groups. Two highlights of this theory are the statement that a finite abelian group is the direct product of its Sylow subgroups, and that it is a direct product of cyclic groups. The first decomposition is unique; the second one is not unique, though there are uniqueness assertions that can be made in connection with it.
Let us explain the first claim of the last paragraph. If $G$ is a finite group, and $p$ a prime dividing $|G|$, we can write $|G| = p^k m$ where $p \nmid m$. Then a subgroup of order $p^k$ is called a $p$-Sylow subgroup (or sometimes a Sylow $p$-subgroup). Later we will prove that all finite groups have $p$-Sylow subgroups for every $p| |G|$, but in this section we will content ourselves to discuss the case where $G$ is abelian. In that case, we will prove that $G$ has a unique $p$-Sylow $G_p$ and that \[ G = \prod_{p| |G|} G_p . \]
If $G$ is a finite abelian group, written additively, \[ \{n \in \mathbb{Z}| n G = 0\} \] is an ideal in $\mathbb{Z}$. Since $\mathbb{Z}$ is a principal ideal domain, this ideal has a generator $d$. Thus \[ \text{$n g = 0$ for all $g \in G$ if and only if $d|n$} . \] (If we were writing the group multiplicatively, we would write $g^n = 1$ instead of $n g = 0$.) The integer $d$ is called the exponent of the finite abelian group $G$.
Proposition 1.3.8: Let $G$ be an abelian group of exponent $m n$ where $m$ and n are coprime integers. Then $G$ has unique subgroups $M$ and $N$ of exponents $m$ and $n$ respectively, and $G = M \oplus N$ (internal direct product).
Proof. (Click to Expand/Collapse)
Let $m_1$ and $n_1$ be the exponents of $M$ and $N$, respectively. We have $m M = m l n G = 0$ since $m n$ is the exponent of $G$, and so $m_1 |m$; similarly $n_1 |n$. On the other hand, \[ m_1 n_1 G = n_1 m_1 M \oplus m_1 n_1 N = 0, \] so $m n$ divides $m_1 n_1$. It follows that $m_1 = m$ and $n_1 = n$.
Now any element $g$ of $G$ can be written as $1 \cdot g = e \cdot g + f \cdot g \in M + N$, so $M + N = G$. On the other hand, $M \cap N = 0$ since if $x \in M \cap N$ we can write $x = e y = f z$, so \[ x = 1 \cdot x = e \cdot x + f \cdot x = e f z + f e y = 0 + 0 = 0. \] This proves that $G = M \oplus N$.
We leave it to the reader to show that $M$ and $N$ are the unique subgroups with exponents $m$ and $n$.
Exercise 1.3.11: Complete the proof of the last Proposition by showing that $M$ and $N$ are the unique subgroups with exponents $m$ and $n$.
Proposition 1.3.9: Let $G$ be a finite abelian group (written additively), and let $p_1, \cdots, p_r$ be the distinct primes dividing the exponent $p_1^{k_1} \cdots p_r^{k_r}$ of $G$. Then $G$ has subgroups $P_1, \cdots, P_r$ such that the exponent of $P_i$ is $p_i^{k_i}$, and $G = P_1 \oplus \cdots \oplus P_r$ (internal direct product).
Proof. (Click to Expand/Collapse)
Proposition 1.3.10: Let \[ 0 \longrightarrow K \mathop{\longrightarrow}\limits^i G \mathop{\longrightarrow}\limits^p Q \longrightarrow 0 \] be a short exact sequence of finite abelian groups, and let $\kappa$, $\gamma$, $\chi$ be the exponents of $K$, $G$ and $Q$, respectively. Then $\kappa$ and $\chi$ divide $\gamma$, and $\gamma$ divides $\kappa \chi$.
Proof. (Click to Expand/Collapse)
A finite group $G$ is called a (finite) $p$-group if its order is a power of $p$.
Proposition 1.3.11: Let $G$ be a finite abelian group, and let $p$ be a prime. Then the order of $G$ is a power of $p$ if and only the exponent of $G$ is a power of $p$.
Proof. (Click to Expand/Collapse)
Thus what we have to show is that, assuming $\gamma$ is a power of $p$, so is $|G|$. By induction, we assume this statement true for all groups of order $< |G|$.
Let $x$ be any nonzero element of $G$. Then $K = \left\langle x \right\rangle$ is a nontrivial normal subgroup of $G$. Since $\gamma$ is a power of $p$, the order of $x$ is a power of $p$, and so the order of $K$ is a power of $p$. Now consider the short exact sequence $0 \longrightarrow K \mathop{\longrightarrow}\limits^i G \mathop{\longrightarrow}\limits^p Q \longrightarrow 0$. The order of $Q$ is smaller than the order of $G$, and its exponent divides $\gamma$, hence is a power of $p$, and so by our inductive hypothesis $|Q|$ is a power of $p$. But now $|G| = |K| |Q|$, so its order is a power of $p$.
We may now prove the existence of Sylow subgroups for finite abelian groups.
Theorem 1.3.1: Let $G$ be a finite abelian group (written additively), and let $p_1, \cdots, p_r$ be the distinct primes dividing the order $p_1^{k_1} \cdots p_r^{k_r}$ of $G$. Then $G$ has subgroups $P_1, \cdots, P_r$ such that the order of $P_i$ is $p_i^{k_i}$, and $G = P_1 \oplus \cdots \oplus P_r$ (internal direct product).
Proof. (Click to Expand/Collapse)
Exercise 1.3.12: Prove that $P_i$ is the unique subgroup of $G$ of order $p_i^{k_i}$.
We have reduced the structure of finite abelian groups to that of finite abelian $p$-groups.
Lemma 1.3.1: Let $P$ be an abelian group of exponent $p^k$, and let $x$ be an element of order exactly $p^k$. Suppose that $P / \left\langle x \right\rangle$ is cyclic, of order $p^r$. Then there exists an element $y$ of $P$ of order $p^r$ such that $P = \left\langle x \right\rangle \oplus \left\langle y \right\rangle$.
Proof. (Click to Expand/Collapse)
Let $z$ be a generator of $P / \left\langle x \right\rangle$, and let $y_1$ be any element of $P$ such that $p (y_1) = z$. The order of $y_1$ is at least $p^r$ (since the order of $z$ is $p^r$) but it might be greater than $p^r$. We will show that there exists another element $y$ of $P$ such that $y_1 - y \in \left\langle x \right\rangle$, so that $p (y) = p (y_1) = z$, and such that the order of $y$ is exactly $p^r$.
Now $\pi (p^r y_1) = p^r \pi (y_1) = p^r z = 0$, so $p^r y_1 \in \ker (\pi) = \left\langle x \right\rangle$. We may thus write $p^r y_1 = m x$ for some $m \in \mathbb{Z}$. Since we have assumed that the exponent of $G$ is $p^k$ we have $r \le k$. We have $p^{k - r} m x = p^k m y_1 = 0$ since $p^k$ is the exponent of $G$. But the order of $x$ is exactly $p^k$, so $p^k$ divides $p^{k - r} m$. This means that $p^r$ divides $m$, and we write $m = p^r m'$. Now let $y = y_1 - m' x$. We see that $y_1 - y \in \left\langle x \right\rangle$, as required. Now we have \[ p^r y = p^r y_1 - p^r m' x = m x - m x = 0, \] so the order of $y$ divides $p^r$. On the other hand, $p^{r - 1} y \neq 0$ since applying $\pi$ gives $p^{r - 1} z \neq 0$. Thus the order of $y$ is precisely $p^r$. Thus $\left\langle z \right\rangle = P / \left\langle x \right\rangle$ and $\left\langle y \right\rangle$ are both cyclic groups of order $p^r$, and there is an isomorphism $s : \left\langle z \right\rangle \longrightarrow \left\langle y \right\rangle$ which gives a splitting of the short exact sequence, so that $P = \left\langle x \right\rangle \oplus \left\langle y \right\rangle$ by Proposition 1.3.3.
Theorem 1.3.2:
Let $P$ be a finite abelian $p$-group. Then $P$ is a direct
product of cyclic groups of prime power order:
\[
P = Z_{p^{k_1}} \oplus Z_{p^{k_2}} \oplus \cdots
\oplus Z_{p^{k_h}} .
\]
(1.3.5)
Proof. (Click to Expand/Collapse)
Therefore, let $x_1$ have order exactly $p^{k_1}$. Then $P / \left\langle x \right\rangle$ is a $p$-group, and its order is strictly less than the order of $P$, so by induction, we may assume that it is a product of cyclic groups, and we obtain a short exact sequence:
| \[ 0 \longrightarrow \left\langle x \right\rangle \longrightarrow P \mathop{\longrightarrow}\limits^{\pi} Z_{p^{k_2}} \oplus \cdots \oplus Z_{p^{k_h}} \longrightarrow 0, \] | (1.3.6) |
We leave the uniqueness assertion to the reader (Exercise 1.3.14).
Exercise 1.3.13: Prove that if $G$ is an abelian group and the exponent of $G$ equals its order, then $G$ is cyclic.
Exercise 1.3.14: Prove that the integers $k_1, k_2, \cdots, k_h$ in Theorem 1.3.2 are uniquely determined by $P$. Equivalently, show that if \[ Z_{p^{k_1}} \oplus \cdots \oplus Z_{p^{k_h}} \cong Z_{p^{l_1}} \oplus \cdots \oplus Z_{p^{l_m}} \] with $k_i$, $l_i > 0$, then $h = m$, and the $k_i$ are the same as the $l_i$, rearranged. (Hint: Define a function $f$ on the positive integers by $f (n) = |p^n P|$. Show that the numbers $k_i$ can be reconstructed from the function $f$.)
Exercise 1.3.15: Show that $G = Z_2 \oplus Z_2$ has three subgroups $H_1, H_2, H_3$ isomorphic to $Z_2$, and that $G$ is the internal direct product of any two. With this in mind, discuss briefly in what sense the decomposition of an abelian $p$-group into a direct product of cyclic groups is unique.
Exercise 1.3.16: Let $G$ be a finite abelian group of exponent $n$. Prove that $G$ has elements of order $n$. (Hint: first do this for $p$-groups, then deduce the general case.)
Exercise 1.3.17: Let $G$ be a finite abelian group. Show that there exists a sequence $m_1, \cdots, m_r$ of integers such that $m_1 |m_2 | \cdots |m_r$ and $G \cong Z_{m_1} \oplus \cdots \oplus Z_{m_r}$, and that the integers $m_i$ are unique.
The last exercises return to the case of a nonabelian group and multiplicative notation to remedy an omission: we have notions of an internal and external direct product, but we have only defined the notion of an internal semidirect product. The external semidirect product is an important construction, but requires a bit more data.
If $G$ is any finite group, an endomorphism, we recall, is a homomorphism $G \longrightarrow G$. If the homomorphism is an isomorphism, it is called an automorphism. The automorphisms form a group, denoted $\operatorname{Aut} (G)$. If $G$ happens to be abelian, the endomorphisms form a ring $\operatorname{End} (G)$, we have already seen, and $\operatorname{Aut} (G)$ is its multiplicative group. If $G$ is nonabelian, there is no longer an additive structure on $\operatorname{End} (G)$, which becomes less important. However $\operatorname{Aut} (G)$ is always important.
Exercise 1.3.18: Show that $\operatorname{Aut} (Z_2 \oplus Z_2)$ is a nonabelian group of order 6. Thus even if $G$ is nonabelian, its automorphism group might be abelian.
Exercise 1.3.19: Show that if $G$ is an abelian group of exponent $n$ and $x, y$ are elements of order $n$ then there exists an automorphism $\sigma \in \operatorname{Aut} (G)$ such that $\sigma (x) = y$. (Hint: first prove this in the case where $G$ is a $p$-group; to accomplish this, observe that in the proof of Theorem 1.3.2, $x$ could be an arbitrary element of order equal to the exponent of $G$, and ponder the consequences.)
Exercise 1.3.20: Show that in $G = Z_4 \oplus Z_2$ there exist two elements $x$ and $y$ of order 2 such that $\sigma (x) \neq y$ for all automorphisms $\sigma \in \operatorname{Aut} (G)$.
We will leave the external semidirect product to exercises. These exercises are extremely important, since they give a powerful tool for constructing groups.
Exercise 1.3.21: Let $G$ be a group, written multiplicatively, with subgroups $H$ and $K$ such that $K$ is normal and $H K = G$, $H \cap K = 1$. Thus $G = K \rtimes H$ (internal semidirect product). Show that there is a homomorphism $\phi : H \longrightarrow \operatorname{Aut} (K)$ defined by $\phi (h) k = h k h^{- 1}$.
Exercise 1.3.22: (External Semidirect Product) Let $H$ and $K$ be groups, and let there be given a homomorphism $\phi : H \longrightarrow \operatorname{Aut} (K)$. As a notational point, we will write $^{\sigma} k$ instead of $\sigma (k)$ when $\sigma \in \operatorname{Aut} (K)$, since this notation is sometimes easier to parse. Construct a group $G = K \rtimes_{\phi} H$ as follows. As a set, $G$ will be the Cartesian product $K \times H$, that is, the set of ordered pairs $(k, h)$ with $k \in K$ and $h \in H$, but the multiplication will be "twisted'' by $\phi$: \[ (k, h) (k', h') = (k \cdot {^{\phi (h)} k'}, h h') . \] Prove that this is a group, and has subgroups $H_1$ and $K_1$ that are isomorphic to $H$ and $K$ respectively, such that $G$ is the internal semidirect product of $K_1$ and $H_1$.
Exercise 1.3.23: Let $ K = Z_7$ be the cyclic group generated by $x$, of order 7. Show that $K$ has an automorphism of order three such that $x \longmapsto x^2$. Deduce that there exists a nonabelian group of order 21.