Examples
We will often describe groups by generators and relations. This mean that we write $G = \left\langle x, y, z, \cdots \right\rangle$ and give enough relations between these that the multiplication table can be completely reconstructed. This is an extremely handy thing to do when actually working with groups.
We will illustrate this with examples. First, the cyclic group $Z_n$ has one generator $x$, and one relation $x^n = 1$. The meaning of this is that the multiplication table can be completely reconstructed from this one rule; so for example if $n = 3$, the rule $x^3 = 1$ is sufficient to imply that $G =\{1, x, x^2 \}$, and second, that (for example $x^2 \cdot x^2 = x$). The set of relations in a description by generators and relations is sometimes called a presentation of the group.
To give a slightly less trivial example, given any $n > 2$, $\operatorname{Aut} (Z_n) \cong (\mathbb{Z}/ n\mathbb{Z})^{\times}$ contains a special element of order $2$, namely the automorphism $\xi \longmapsto \xi^{- 1}$, corresponding to $- 1$ in the multiplicative group $(\mathbb{Z}/ n\mathbb{Z})^{\times}$. Let $\theta : Z_2 \longrightarrow \operatorname{Aut} (Z_n)$ be the homomorphism mapping the generator of $Z_2$ to this automorphism. The semidirect product $Z_n \rtimes_{\theta} Z_2$ is called the dihedral group $D_{2 n}$.
- The group $D_{2 n}$ has generators and relations $x$ and $y$ satisfying $x^n = y^2 = 1$ and $y x y^{- 1} = x^{- 1}$.
To see how these relations are derived from our original description of the group as a semidirect product, we recall from Exercise 1.3.22 that $Z_n \rtimes_{\theta} Z_2$ is the set of ordered pairs $(k, h)$ with $k \in Z_n$ and $h \in Z_2$ and multiplication \[ (k, h) (k', h') = (k \cdot {^{\theta (h)} k'}, h h') . \] If $x$ is a generator of $Z_n$ and $y$ is a generator of $Z_2$, then we may identify $x$ and $y$ with their images in $Z_n \rtimes_{\theta} Z_2$. Thus we identify $x \longleftrightarrow (x, 1)$ and $y \longleftrightarrow (1, y)$. Then we compute \[ (1, y) (x, 1) (1, y) = (^{\theta (y)} x, y) (1, y) = (x^{- 1}, y) (1, y) = (x^{- 1} \cdot^{\theta (y)} 1, y^2) = (x^{- 1}, 1), \] which gives the relation $y x y^{- 1} = x^{- 1}$.
Remark 1.7.1: In practice, it is straightforward, given groups $K$ and $H$ described by generators and relations, and a homomorphism $\phi : H \to \operatorname{Aut} (K)$ to write down generators and relations for $K \rtimes_{\phi} H$. One takes the union of the generators for $H$ and the generators for $K$, and for each pair of generators $x \in K$ and $y \in H$ we append the relation $y x y^{- 1} = {^{\phi (y)} x}$, where we write out $^{\phi (y)} x \in K$ in terms of the given generators of $K$.
This is exactly what we did in the above discussion of $D_{2 n}$. We will give another example of this procedure shortly below, but we are not quite finished discussing the example of $D_{2 n}$, to which we return.
To see that this presentation is determines the multiplication table of $D_{2 n}$, we observe that given these relations, the set of $2 n$ elements \[ S =\{1, x, x^2, \cdots, x^{n - 1}, y, x y, x^2 y, \cdots, x^{n - 1} y\} \] is closed under multiplication. For example we use the relations we can compute \[ y x^k \cdot y x^l = x^{- k + l} = x^r \] where $r$ is the remainder of $- k + l$ on division by $n$. One may also use the relations to see that $S$ is closed under inverses – for example $( x^k y)^2 = x^k x^{- k} y^2 = 1.$, so $(x^k y)^{- 1} = x^k y$. Once we see that $S$ is closed under multiplication and contains both generators $x$ and $y$, it follows that $S$ is a group and contains the generators, so $S = G$.
However the insight that the rules $x^n = y^2 = 1$ and $y x y^{- 1} = x^{- 1}$ are sufficient to show that $|G| = 2 n$ by exhibiting $2 n$ elements that exhaust the group, they are not sufficient to show that there exists a group of order $2 n$ with these generators and relations. In other words, we proved that $|G| \le 2 n$ using just the relations but we did not prove that $|G| \ge 2 n$ using the relations – for that, we relied on the the semidirect product.
For example, here is a presentation of the nonabelian group with 21 elements. (See Exercise 1.3.23 and Proposition 1.7.1 below.)
- The group $G$ has generators $x$ and $y$ with relations $x^7 = y^3 = 1$ and $y x y^{- 1} = x^2$.
Exercise 1.7.1: Imitate the above discussion of $D_{2 n}$ and show that the set \[ S =\{x^a y^b |0 \le a < 7, 0 \le b < 3\} \] is closed under multiplication and inverses, and deduce that $S = G$, so that $|G| \le 21$.
Note that this reasoning does not prove that a group $G$ of order 21 with these generators and relations exists, because it does not prove that all 21 elements listed in $S$ are distinct from each other.
To see that this is a real issue, we can define a group with the following generators and relations:
- This group $G'$ has generators $z$ and $w$ with relations $z^5 = y^3 = 1 \operatorname{and} y z y^{- 1} = x^3$.
So $G'$ is a nonabelian group of order 15! Right?
Wrong! We will see in Proposition 1.7.1 that there is no nonabelian group of order $15$!
The problem is that the relations can be used to show that the elements in $S'$ are not all distinct. Indeed, $y^3 = 1$ so \begin{eqnarray*} x = y^3 x y^{- 3} = y^2 (y x y^{- 1}) y^{- 2} = y^2 x^3 y^{- 2} = y (y x^3 y^{- 1}) y^{- 1} & = & \\ y (y x y^{- 1})^3 y^{- 1} = y x^9 y^{- 1} & = & x^{27} \end{eqnarray*} So $x^{26} = 1$; but $x^5 = 1$ and so $x = x \cdot (x^5)^5 = x^{26} = 1$, and so the elements in $S'$ are definitely not distinct.
Now let us return to the "real'' group of order 21 whose existence is proved by exhibiting a homomorphism $\theta : Z_3 = \left\langle y \right\rangle \longrightarrow \operatorname{Aut} \left( Z_7 \right.$) where $Z_7 = \left\langle x \right\rangle$. The homomorphism $\theta$ can be chosen so that $\theta (y)$ is the automorphism $x \mapsto x^3$ of $Z_7$. Then Remark 1.7.1 gives a prescription for generators and relations for the semidirect product $Z_7 \rtimes_{\theta} Z_3$. We start with the relations describing $Z_7$ and $Z_3$: \[ x^7 = 1, \hspace{2em} y^3 = 1. \] Then, Remark 1.7.1 tells us to add the single relation \[ y x y^{- 1} = x^2 \] to obtain a presentation of $G$.
Now let us classify groups of order $p q$ where $p$ and $q$ are distinct primes.
Proposition 1.7.1: Let $|G| = p q$ where $p$ and $q$ are distinct primes. We assume without loss of generality that $p < q$. Then $G$ has a normal $q$-Sylow subgroup $Q$; if $P$ is a $p$-Sylow then $G$ is the semidirect product of $Q \ltimes P$. If $p \nmid q - 1$ then $G$ is cyclic. If $p|q - 1$ then there is a nonabelian group of order $p q$, unique up to isomorphism, namely $Z_q \rtimes_{\theta} Z_p$, where $\theta : Z_p \longrightarrow \operatorname{Aut} (Z_q) \cong Z_{q - 1}$ is a nontrivial homomorphism.
Proof. (Click to Expand/Collapse)
The group $G$ is determined by a homomorphism $\theta : P \longrightarrow \operatorname{Aut} (Q)$. Now $P \cong Z_p$ and By Proposition 1.5.5 and Theorem 1.5.2 $\operatorname{Aut} (Q) \cong (\mathbb{Z}/ q\mathbb{Z})^{\times} \cong Z_{q - 1}$. If $p \nmid q - 1$ then the only homomorphism $Z_p \longrightarrow Z_{q - 1}$ is the trivial map; and if $\theta$ is trivial then $Z_q \rtimes_{\theta} Z_p$ is just the direct product $Z_q \times Z_p \cong Z_{p q}$.
On the other hand, if $p \nmid q - 1$ there are nontrivial homomorphisms $\theta : Z_p \longrightarrow Z_{q - 1}$. There are more than one, so one might imagine that there is more than one isomorphism class of semidirect product. However, these groups are all isomorphic, and this may be seen as follows. First, $Z_{q - 1}$ has a unique subgroup, and this must be the image of $\theta$. Now any two nontrivial homomorphisms $\theta, \theta' : Z_p \longrightarrow Z_{q - 1}$ must differ by an automorphism of $Z_p$; that is, there is an automorphism $\alpha : Z_p \longrightarrow Z_p$ such that $\theta' = \theta \circ \alpha$. Now $\alpha$ induces an isomorphism $Z_q \ltimes_{\theta} Z_p \longrightarrow Z_q \ltimes_{\theta'} Z_p$; so there is but one such semidirect product.
We turn next to the alternating groups. The symmetric group has an important subgroup of index two, the alternating group $A_n$. We can construct it by means of a group action. Let $S_n$ act on polynomials in $n$ indeterminates $X_1, \cdots, X_n$ by permuting the indices: thus if $p \in \mathbb{C}[X_1, \cdots, X_n]$ and $\sigma \in S_n$ let
| \[ \sigma p (X_1, \cdots, X_n) = p (X_{\sigma (1)}, \cdots, X_{\sigma (n)}) . \] | (1.7.1) |
Exercise 1.7.2: Prove that if $\sigma = (i_1, \cdots, i_r)$ is an $r$-cycle then $\varepsilon (\sigma) = (- 1)^{r - 1}$. (Hint: since $\varepsilon$ is a homomorphism to an abelian group, it is constant on conjugacy classes. Thus we may assume that $\sigma = (1, 2, \cdots, r)$, in which case show that there are exactly $r - 1$ pairs $(i, j)$ with $i < j$ and $\sigma (j) < \sigma (i)$.)
Exercise 1.7.3: Show that $\varepsilon (\sigma)$ can be computed by counting the number of cycles of even length in the decomposition of $\sigma$ into a product of disjoint cycles; if there are an even number of these, then $\varepsilon (\sigma) = 1$, otherwise $\varepsilon (\sigma) = - 1$.
The kernel of $\varepsilon$ is a subgroup of index two, the alternating group. It is normal, being the kernel of a homomorphism, but it is worth noting that a subgroup of index two is always normal – see Exercise 1.7.4.
Exercise 1.7.4: Show that any subgroup $H$ of $G$ of index two is normal. (Hint: if $x \in G$ but $x \in H$, then $x H = H x$ since $x H$ is the set-theoretic complement $G - H$, and so is $H x$.)
The alternating groups are important examples of simple groups. A group $G$ is called simple if its only normal subgroups are $1$ and $G$. Simple groups can be considered the basic building blocks from which all groups are built up. The reason for this has to do with the Jordan-Hölder Theorem, which we will not prove, but which we now state. A normal series of length r for a group $G$ is a sequence of subgroups \[ 1 = G_0 \subsetneq G_1 \subsetneq G_2 \subsetneq \cdots \subsetneq G_r = G \] such that $G_{i - 1}$ is normal in $G_i$; it is called a composition series if $G_i / G_{i - 1} = Q_i$ is a simple group. We think of $G$ as being built up from the simple groups $Q_1, Q_2, \cdots, Q_r$, which are called the composition factors.
Theorem 1.7.1: (Jordan-Hölder.) Any finite group has at least one composition series. Any two composition series for $G$ have the same length and (up to isomorphism) the same quotients $Q_1, Q_2, \cdots, Q_r$, though they can occur in a different order. Each simple group appears the same number of times in both composition series.
Proof. (Click to Expand/Collapse)
If we have a short exact sequence: \[ 1 \longrightarrow N \longrightarrow G \longrightarrow Q \longrightarrow 1, \] then the composition factors of $G$ are the union of the composition factors of $N$ and $Q$, and the number of times a composition factor appears in a composition series for $G$ is the sum of the number of times that it appears in the composition series for $N$ and for $Q$. We think of $G$ being broken down into smaller pieces, in this case $N$ and $Q$. Now $N$ and $Q$ may themselves be further broken down until no further normal subgroups can be found among any of the resulting pieces, which are thus simple, and these are the composition factors. The Jordan-Hölder Theorem assures us that we will find the same basic "atoms'' no matter how $G$ is thus broken down. This is similar to the situation in Chemistry when it was discovered that matter had irreducible constuents, and anything you did to a chemical did not change its constutuent atoms. Simple groups are thus the "atoms'' in group theory.
The composition factors are key invariants of the group. Thus simple groups are very special and important. Remarkably, they have been classified: it was shown around 1980 as the work of many people that the simple groups are the groups $Z_p$ when $p$ is prime, $A_n$ (except $A_4$, which is not simple); various infinite series of linear groups; and 26 sporadic simple groups that do not fit into any of these infinite families.
It is true that once one knows all simple groups, one still does not in any sense know all the groups, since the "extension'' $1 \longrightarrow N \longrightarrow G \longrightarrow Q \longrightarrow 1$ may not be a direct product, or even a semidirect product. Information is lost in breaking the group down into its simple constituents. Still, there is a sense that since the finite simple groups have been classified, groups are now understood in a much better way. The atoms have all been discovered.
The fact that $G = Z_p$ is simple when $p$ is prime is obvious since it has no subgroups at all (let alone normal ones) except $1$ and $G$.
The group $S_4$ has a normal subgroup of order $4$, namely \[ V = \left\{ 1, (12) (34), (13) (24), (14) (23)\}, \right. \] known as Klein's Viergruppe. It is obviously a union of conjugacy classes, so obviously normal. Since it is contained in $A_4$, the group $A_4$ is not normal. But $A_5$ is, and this is quite easy to check.
Proposition 1.7.2: The group $A_5$ is simple.
This is a special case of the next theorem, but we'll prove this special case more thoroughly.
Proof. (Click to Expand/Collapse)
Theorem 1.7.2: The group $A_n$ is simple when $n \ge 5$.
Proof. (Click to Expand/Collapse)
Exercise 1.7.5: Complete this outline to a proof that $A_n$ is simple if $n \ge 5$.
Theorem 1.7.3: If $q > 3$ the group $\operatorname{PSL}_2 (\mathbb{F}_q)$ is simple.
The following sketch is not intended to be full enough to give more than a general idea of how this is proved.
Proof. (Click to Expand/Collapse)
The reader may have been surprised by the table in the proof of Proposition 1.7.2, since $(12345)$ are conjugate in $S_5$ but not its subgroup $A_5$. We note that the conjugacy class of 5-cycles in $S_5$ split cleanly into two $A_5$ conjugacy classes of the same size. It is worth noting that this is a special case of a general phenomenon, and the proof is a good example of the use of ideas originating in Theorem 1.5.1.
Proposition 1.7.3: Let $G$ be a group and $N$ a subgroup of index two. Every conjugacy class $\mathcal{C}$ of $G$ that is contained in $N$ is either also an $N$-conjugacy class or splits into two $N$-conjugacy classes of equal size. Let $x \in \mathcal{C}$; by assumption $\mathcal{C} \subset N$ so $x \in N$ also. If the centralizer $C_G (x)$ is contained in $N$, then $\mathcal{C}$ splits into two $N$-conjugacy classes; otherwise, it is itself an $N$-conjugacy class.
Proof. (Click to Expand/Collapse)
If the image of the restriction of $\phi$ to $C_G (x)$ is $Z_2$, then its kernel has index 2 so $[C_G (x) : C_N (x)] = 2$ and the number of $N$-conjugates of $x$ is \[ [N : C_N (x)] = \frac{1}{2} [G : C_N (x)] = \frac{1}{2} [C_G (x) : C_N (x)] [G : C_G (x)] = [G : C_G (x)] = |\mathcal{C}|. \] In this case, the set of $N$-conjugates agrees with the set of $G$-conjugates.
The image is $1$ if and only if $C_N (x) \subset N$ and so $C_N (x) = C_G (x)$. The number of $N$-conjugates of $x$ is \[ [N : C_N (x)] = \frac{1}{2} [G : C_N (x)] = \frac{1}{2} [G : C_G (x)] = \frac{1}{2} |\mathcal{C}|. \] Thus the set of $N$-conjugates is half the size of the set of $G$-conjugates. The same reasoning must apply to the other $N$-conjugacy classes that are contained in $\mathcal{C}$, so obviously $\mathcal{C}$ splits into two classes of equal size.
Exercise 1.7.6: Show that a conjugacy class of $S_n$ that is contained in $A_n$ splits into two $A_n$ conjugacy classes if and only if when a representative is written as a product of disjoint cycles, the cycles that appear are all of odd length and no two have the same length. Decide which conjugacy classes of even permutations in $S_9$ split into two $A_9$-conjugacy classes.
Another important fact about $A_5$ is that it is the rotation group of the icosahedron. How can we see this? The group $G$ of rotations of the icosahedron has 3 transitive actions that present themselves.
- First, on the 12 vertices. The stabilizer of a vertex is the group of rotations that fixes it, obviously of order 5, and so by Theorem 1.5.1, the order of the group is determined by the fact that the index of this stabilizer is 12, so $|G| = 60$.
- Or, on the 30 edges. The stabilizer of an edge clearly has order 2, so again Theorem 1.5.1 allows us to compute $|G| = 60$.
- Or, on the 20 faces. The stabilizer of a face has order 3, so again Theorem 1.5.1 allows us to compute $|G| = 60$.
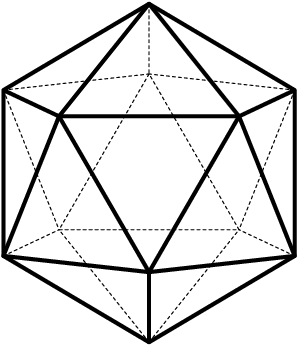
|
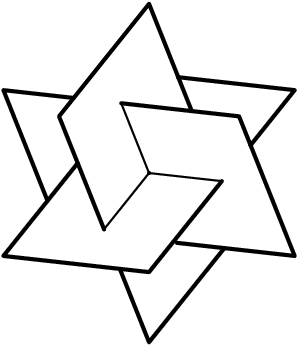
|
| \[ \begin{array}{l} \text{The icosahedron and one of 5 figures consisting of}\\ \text{3 perpendicular inscribed golden rectangles.} \end{array} \] | (1.7.2) |
Two opposite edges of the icosahedron span a rectangle, and we may collect three of these rectangles that intersect perpendicularly at the center, as in Figure 1.7.2. It may be shown that these rectangles have sides in the ratio $\frac{1 + \sqrt{5}}{2} = 1.618 \cdots$, the so-called "Golden Ratio.'' This is close enough to $5 / 3 = 1.666 \cdots$ that a good model of this configuration can be made with three $3 \times 5$ cards.
As there are 5 such configurations inscribed in the icosahedron, the group of rotations of the icosahedron acts on them, transitively, and so by Theorem 1.5.1 we obtain a homomorphism of $G$ into $S_5$, and the image of this homomorphism may be seen to be $A_5$.
Exercise 1.7.7: Show that the rotation groups of the tetrahedron and octahedron (or cube) are $A_4$ and $S_4$ respectively. Explain why the rotation groups of the octahedron and of the cube are the same.
We turn now to ubiquity of semidirect products. It turns out that every group of order $< 24$ is either cyclic, or a $p$-group for some $p$ or is a semidirect product of Sylow subgroups. Presently we will confirm this by investigating groups of the various orders. Semidirect products account for a great many groups.
Proposition 1.7.4: A group $G$ of order $12$ is a semidirect product of Sylow subgroups.
Proof. (Click to Expand/Collapse)
Exercise 1.7.8: Show that a group of order 56 is a semidirect product of Sylow subgroups.
We may now construct the nonabelian groups of order 12. First suppose that there is a normal 3-Sylow $Q$. Its automorphism group $\operatorname{Aut} (Q)$ is of order 2. The $2$-Sylow $P$ may be $Z_4$ or $Z_2 \times Z_2$, and in either case there is a nontrivial homomorphism $\theta : P \longrightarrow \operatorname{Aut} (Q)$ that is unique up to an automorphism of $P$. There are therefore two nonabelian groups with normal $3$-Sylow. They can be described by generators and relations.
- The first, with $P \cong Z_4$ has generators $x$ and $y$ such that $x^3 = y^4 = 1$ and $y x y^{- 1} = x^{- 1}$. Thus $P = \left\langle y \right\rangle$ and $Q = \left\langle x \right\rangle$.
- The second, with $P \cong Z_2 \times Z_2$ has generators $x, y, z$ such that $x^3 = y^2 = z^2$, $y z = z y$ and $y x y^{- 1} = x^{- 1}$, $z x z^{- 1} = z$. Thus $P = \left\langle y, z \right\rangle$ and $Q = \left\langle x \right\rangle$.
- $G$ has generators $x, y, z$ such that $x^3 = y^2 = z^2$, $y z = z y$ and $x y x^{- 1} = z,$ $x z x^{- 1} = y z$ and $x y z x^{- 1} = y$.
We have seen that any group of order $p^k$ with $k \le 2$ is abelian. For order $p^3$, there are two $p$-groups, and as $k$ increases the number of groups of order $p^k$ proliferates; for example, if $k \ge 5$ the number of groups of order $p^k$ goes to infinity as $p \longrightarrow \infty$. However the groups of order $p^3$ are worth knowing, and we look at these next.
It turns out that the case $p = 2$ is different. The two nonisomorphic nonabelian groups of order $8$ are the dihedral group $D_8$, which we have already met, and the quaternion group $Q_8$ which is related to Hamilton's quaternion algebra $\mathbb{H}$, a famous ring. The group $Q_8$ can be embedded conveniently into $\mathbb{H}^{\times}$, so first let us construct $\mathbb{H}$.
We recall an algebra over a field $F$ is a ring containing $F$ in its center; thus it becomes a vector space over $F$. The algebra $\mathbb{H}$ over $\mathbb{R}$ is a four-dimensional real vector space with basis elements $1, i, j, k$. Thus $\mathbb{R} \cdot 1$ is the subring $\mathbb{R}$, which coincides with the center of $\mathbb{H}$. The basis elements satisfy the relations $i^2 = j^2 = k^2 = - 1$, $i j = - i j = k$, $j k = - k j = i$ and $k i = - i k = j$.
To show that a four-dimensional associative algebra with this description actually exists, one method is to consider the subring of $\operatorname{Mat}_2 (\mathbb{C})$ generated by \[ 1 = \left(\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right), \hspace{2em} i = \left(\begin{array}{cc} i & 0\\ 0 & - i \end{array}\right), \hspace{2em} j = \left(\begin{array}{cc} 0 & 1\\ - 1 & 0 \end{array}\right), \hspace{2em} k = \left(\begin{array}{cc} 0 & i\\ i & 0 \end{array}\right) . \] We are abusing notation by using the same letter $i$ to denote both the complex number $\sqrt{- 1}$ and the given matrix. The reader will easily check that these 4 matrices satisfy the required identities, and they span a 4-dimensional real subspace of $\operatorname{Mat}_2 (\mathbb{C})$ that is closed under multiplication, that is, an $\mathbb{R}$-algebra.
The eight quaternions $\pm 1, \pm i, \pm j, \pm k$ form a subgroup of $\mathbb{H}^{\times}$, which is the second nonabelian subgroup of the dihedral group. This group contains only 1 element of order 2 but 6 of order 4, whereas $D_8$ has 2 elements of order 4 and 5 of order 2, so the groups are not isomorphic. Here is a presentation of $Q_8$.
- $Q_8$ has generators $x$ and $y$ subject to the identities $x^4 = y^4 = 1$, $y x y^{- 1} = x^{- 1}$ and $y^2 = x^2$.
Exercise 1.7.9: Show that in the group described by the above generators and relations, the set $\{1, x, x^2, x^3, y, y x, y x^2, y x^3\}$ is closed under multiplication and inverses, and deduce that these relations are a presentation of $Q_8$.
If $p$ is odd, there are again 2 nonisomorphic subgroups of order $p$. First, there is one in which every element but the identity has order $p$; there is also one in which there are some elements of order $p^2$. To construct a nonabelian group of order $p^3$ in which there are elements of $p^2$, observe that by Proposition 1.5.5 $\operatorname{Aut} (Z_{p^2}) \cong \mathbb{Z}/ p^2 \mathbb{Z}$ has order $p^2 - p = p (p - 1)$, so it has a subgroup of order $p$. Thus there is a nontrivial homomorphism $\theta : Z_p \longrightarrow \operatorname{Aut} (Z_{p^2})$ and we can construct the semidirect product $Z_{p^2} \rtimes Z_p$.
To give generators and relations for this group, let us find an explicit element of order $p$ in $\operatorname{Aut} (Z_{p^2}) \cong \mathbb{Z}/ p^2 \mathbb{Z}$. We can take $1 + p \in \mathbb{Z}/ p^2 \mathbb{Z}$. By the binomial theorem, \[ $(1 + p)^p = 1 + \binom{p}{1} p + \binom{p}{2} p^2 + \ldots p^p \equiv 1\quad\operatorname{mod}\quad p^2, \] so $1 + p$ will work. If $x$ is a generator for $Z_{p^2}$, then under the corresponding automorphism $x \longmapsto x^{1 + p}$. If $y$ is a generator for $Z_p$, then we may map $y$ to this automorphism under the map $\theta$.
\[ \left\langle x, y|x^{p^2} = y^p = 1, y x y^{- 1} = x^{1 + p} \right\rangle . \] This is a more compact notation indicating that the group has the given generators and relations.
To construct a nonabelian group of order $p^3$ in which every nonidentity element has order $p$, start with $Z_p \times Z_p$, and observe that by Proposition 1.5.8 $\operatorname{Aut} (Z_p \times Z_p) \cong \operatorname{GL}_2 (\mathbb{F}_p)$, which contains elements of order $p$. Indeed, this group has order $(p^2 - 1) (p^2 - p)$ has order a multiple of $p$, so the existence of elements of order $p$ follows from the Sylow theorem (or Proposition 1.5.3). Or more directly, one may exhibit an element of order $p$ in $\operatorname{GL}_2 (\mathbb{F}_p)$ directly, namely the matrix $\left(\begin{array}{cc} 1 & 1\\ 0 & 1 \end{array}\right)$. Thus we have a homomorphism $\theta : Z_p \longrightarrow \operatorname{Aut} (Z_p \times Z_p)$, and we may construct the semidirect product. We may take as generators and relations for the group $Z_p \times Z_p$ elements $x, y$ with relations $x^p = y^p = 1$ and $x y = y x$. The automorphism corresponding to $\left(\begin{array}{cc} 1 & 1\\ 0 & 1 \end{array}\right)$ then has the effect $x \longmapsto x$ and $y \longmapsto x y$, if we identify $x$ and $y$ with the vectors $\left(\begin{array}{c} 1\\ 0 \end{array}\right)$ and $\left(\begin{array}{c} 1\\ 1 \end{array}\right)$ in $\mathbb{F}_p^2$ as in the proof of Proposition 1.5.8. We can take a generator $z \in Z_p$ and map this to this automorphism under the map $\theta$. Thus we obtain the presentation \[ \left\langle x, y, z|x^p = y^p = z^p = 1, x y = y x, z x z^{- 1} = x, z y z^{- 1} = x y \right\rangle . \]
We explained this method of construction in order to give another illustration of how one thinks about semidirect products. But we can give a more direct construction as follows. Let $G$ be the subgroup of elements of $\operatorname{GL}_3 (\mathbb{F}_p)$ of the form \[ \left(\begin{array}{ccc} 1 & t & u\\ & 1 & v\\ & & 1 \end{array}\right) . \] (Any entry not written is assumed to be zero.) In this group, we consider the following elements \[ x = \left(\begin{array}{ccc} 1 & & 1\\ & 1 & \\ & & 1 \end{array}\right), \hspace{2em} y = \left(\begin{array}{ccc} 1 & & \\ & 1 & 1\\ & & 1 \end{array}\right), \hspace{2em} z = \left(\begin{array}{ccc} 1 & 1 & \\ & 1 & \\ & & 1 \end{array}\right) . \] One checks easily that these satisy the relations \[ x^p = y^p = z^p = 1, \hspace{2em} x y = y x, \hspace{2em} z x z^{- 1} = x, \hspace{2em} z y z^{- 1} = x y, \] so this gives a second concrete realization of the group, independent of the semidirect product construction, proving existence.
It may still not be obvious that every nonidentity element in this group has order $p$. Using this matrix realization, we may prove it as follows. One checks by induction that \[ {\left(\begin{array}{ccc} 1 & t & u\\ & 1 & v\\ & & 1 \end{array}\right)}^k = {\left(\begin{array}{ccc} 1 & k t & k u + \frac{1}{2} k (k - 1) t v\\ & 1 & k v\\ & & 1 \end{array}\right)} . \] \[ \] In particular, if $k = p$, this becomes the identity since $\frac{1}{2} p (p - 1)$ is a multiple of $p$. Note that this is the only place in the whole discussion that we have used the assumption that $p$ is odd. But if $p = 2$, then $\frac{1}{2} p (p - 1)$ is not a multiple of $2$, and so this argument breaks down – and indeed, if $p = 2$ then every nonabelian group of order $8$ is either $D_8$ or $Q_8$, and has elements of order 4.
Exercise 1.7.10: Prove that every group of order $p^3$ is one of the ones discussed above.
Exercise 1.7.11: Prove that any group of order $18$ has a normal $3$-Sylow subgroup and is a semidirect product. Construct two nonisomorphic nonabelian groups of order $18$.
Exercise 1.7.12: Prove that any group of order $20$ has a normal $5$-Sylow subgroup and is a semidirect product. Construct two nonisomorphic nonabelian groups of order $20$.