You can create Weyl groups and affine Weyl groups for any root system. A variety of methods are available for these. Some of these are methods are available for general Coxeter groups.
By default, elements of the Weyl group are represented as matrices:
sage: WeylGroup("A3").simple_reflection(1)
[0 1 0 0]
[1 0 0 0]
[0 0 1 0]
[0 0 0 1]
You may prefer a notation in which elements are written out as products of simple reflections. In order to implement this you need to specify a prefix, typically "s":
sage: W = WeylGroup("A3",prefix="s")
sage: [s1,s2,s3]=W.simple_reflections()
sage: (s1*s2*s1).length()
3
sage: W.long_element()
s1*s2*s3*s1*s2*s1
sage: s1*s2*s3*s1*s2*s1 == s3*s2*s1*s3*s2*s3
True
The Weyl group acts on the ambient space, which is
available as a space(). To illustrate this, recall
that if 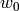 is the long element then
is the long element then 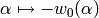 is a permutation of the simple roots. We may compute this
as follows:
is a permutation of the simple roots. We may compute this
as follows:
sage: W = WeylGroup("E6",prefix="s")
sage: w0 = W.long_element(); w0
s1*s3*s4*s5*s6*s2*s4*s5*s3*s4*s1*s3*s2*s4*s5*s6*s2*s4*s5*s3*s4*s1*s3*s2*s4*s5*
s3*s4*s1*s3*s2*s4*s1*s3*s2*s1
sage: sr = W.space().simple_roots().list(); sr
[(1/2, -1/2, -1/2, -1/2, -1/2, -1/2, -1/2, 1/2), (1, 1, 0, 0, 0, 0, 0, 0),
(-1, 1, 0, 0, 0, 0, 0, 0), (0, -1, 1, 0, 0, 0, 0, 0), (0, 0, -1, 1, 0, 0, 0, 0),
(0, 0, 0, -1, 1, 0, 0, 0)]
sage: [-w0.action(a) for a in sr]
[(0, 0, 0, -1, 1, 0, 0, 0), (1, 1, 0, 0, 0, 0, 0, 0), (0, 0, -1, 1, 0, 0, 0, 0),
(0, -1, 1, 0, 0, 0, 0, 0), (-1, 1, 0, 0, 0, 0, 0, 0),
(1/2, -1/2, -1/2, -1/2, -1/2, -1/2, -1/2, 1/2)]
We may ask when this permutation is trivial. If it is nontrivial it induces an automorphism of the Dynkin diagram, so it must be nontrivial when the Dynkin diagram has no automorphism. But if there is a nontrivial automorphism, the permutation might or might not be trivial:
sage: def roots_not_permuted(ct):
....: W = WeylGroup(ct)
....: w0 = W.long_element()
....: sr = W.space().simple_roots()
....: return all(a == -w0.action(a) for a in sr)
....:
sage: for ct in [CartanType(['D',r]) for r in [2..8]]:
....: print ct,roots_not_permuted(ct)
....:
['D', 2] True
['D', 3] False
['D', 4] True
['D', 5] False
['D', 6] True
['D', 7] False
['D', 8] True
If 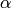 is a root let
is a root let 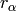 denote the reflection
in the hyperplane of the ambient space that is orthogonal
to
denote the reflection
in the hyperplane of the ambient space that is orthogonal
to 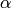 . We reserve the notation
. We reserve the notation 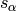 for
the simple reflections, that is, the case where
for
the simple reflections, that is, the case where 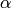 is a simple
root. The reflections are just the conjugates of the simple
reflections.
is a simple
root. The reflections are just the conjugates of the simple
reflections.
The reflections are the keys in a finite family, which is a wrapper around a python dictionary. The values are the positive roots, so given a reflection, you can look up the corresponding root. If you want a list of all reflections, use the method keys() for the family of reflections:
sage: W = WeylGroup("B3",prefix="s")
sage: [s1,s2,s3] = W.simple_reflections()
sage: ref = W.reflections(); ref
sage: Finite family {s1*s2*s1: (1, 0, -1), s2: (0, 1, -1), s3*s2*s3: (0, 1, 1),
s3*s1*s2*s3*s1: (1, 0, 1), s1: (1, -1, 0), s2*s3*s1*s2*s3*s1*s2: (1, 1, 0),
s1*s2*s3*s2*s1: (1, 0, 0), s2*s3*s2: (0, 1, 0), s3: (0, 0, 1)}
sage: ref[s3*s2*s3]
(0, 1, 1)
sage: ref.keys()
[s1*s2*s1, s2, s3*s2*s3, s2*s3*s1*s2*s3*s1*s2, s1, s3*s1*s2*s3*s1, s1*s2*s3*s2*s1, s2*s3*s2, s3]
If instead you want a dictionary whose keys are the roots and whose values are the reflections, you may use the inverse family:
sage: altref=W.reflections().inverse_family(); altref
Finite family {(1, 0, 0): s1*s2*s3*s2*s1, (1, 0, 1): s3*s1*s2*s3*s1, (0, 1, 0): s2*s3*s2,
(0, 1, -1): s2, (1, 0, -1): s1*s2*s1, (0, 1, 1): s3*s2*s3, (1, 1, 0): s2*s3*s1*s2*s3*s1*s2,
(0, 0, 1): s3, (1, -1, 0): s1}
sage: [a1,a2,a3]=W.space().simple_roots()
sage: a1+a2+a3
(1, 0, 0)
sage: altref[a1+a2+a3]
s1*s2*s3*s2*s1
The Weyl group is implemented as a GAP Matrix group. You therefore can display its character table. The character table is returned as a string, which you can print:
sage: print WeylGroup("D4").character_table()
CT1
2 6 4 5 1 3 5 5 4 3 3 1 4 6
3 1 . . 1 . . . . . . 1 . 1
1a 2a 2b 6a 4a 2c 2d 2e 4b 4c 3a 4d 2f
X.1 1 1 1 1 1 1 1 1 1 1 1 1 1
X.2 1 -1 1 1 -1 1 1 -1 -1 -1 1 1 1
X.3 2 . 2 -1 . 2 2 . . . -1 2 2
X.4 3 -1 3 . -1 -1 -1 -1 1 1 . -1 3
X.5 3 -1 -1 . 1 3 -1 -1 -1 1 . -1 3
X.6 3 1 3 . 1 -1 -1 1 -1 -1 . -1 3
X.7 3 1 -1 . -1 3 -1 1 1 -1 . -1 3
X.8 3 -1 -1 . 1 -1 3 -1 1 -1 . -1 3
X.9 3 1 -1 . -1 -1 3 1 -1 1 . -1 3
X.10 4 -2 . -1 . . . 2 . . 1 . -4
X.11 4 2 . -1 . . . -2 . . 1 . -4
X.12 6 . -2 . . -2 -2 . . . . 2 6
X.13 8 . . 1 . . . . . . -1 . -8
Affine Weyl Groups may be created the same way. You simply begin with an affine Cartan type:
sage: W = WeylGroup(['A',2,1],prefix="s")
sage: W.cardinality()
+Infinity
sage: [s0,s1,s2]=W.simple_reflections()
sage: s0*s1*s2*s1*s0
s0*s1*s2*s1*s0
The affine Weyl group differs from a classical Weyl group since it is infinite. The associated classical Weyl group is a subgroup that may be extracted as follows:
sage: W = WeylGroup(['A',2,1],prefix="s")
sage: W1=W.classical(); W1
Parabolic Subgroup of the Weyl Group of type ['A', 2, 1] (as a matrix group
acting on the root space)
sage: W1.simple_reflections()
Finite family {1: s1, 2: s2}
Although W1 in this example is isomorphic to WeylGroup(“A2”) it has a different matrix realization:
sage: for s in WeylGroup(['A',2,1]).classical().simple_reflections():
....: print s
....: print
....:
[ 1 0 0]
[ 1 -1 1]
[ 0 0 1]
[ 1 0 0]
[ 0 1 0]
[ 1 1 -1]
sage: for s in WeylGroup(['A',2]).simple_reflections():
....: print s
....: print
....:
[0 1 0]
[1 0 0]
[0 0 1]
[1 0 0]
[0 0 1]
[0 1 0]
The Bruhat partial order on the Weyl group may be defined as follows.
If 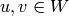 , find a reduced expression of
, find a reduced expression of  into a product
of simple reflections:
into a product
of simple reflections: 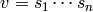 . (It is not assumed
that the
. (It is not assumed
that the 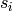 are distinct.) If omitting some of the
are distinct.) If omitting some of the 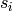 gives a product that represents
gives a product that represents 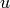 , then
, then 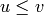 .
.
The Bruhat order is implemented in Sage as a method of Coxeter groups, and so it is available for Weyl groups, classical or affine.
If 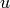 ,
, 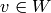 then u.bruhat_le(v) returns true of
then u.bruhat_le(v) returns true of
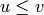 in the Bruhat order.
in the Bruhat order.
If 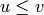 then The Bruhat interval
then The Bruhat interval ![[u,v]](_images/math/9efeb253b42a2c23e3861fab7e820e757e386961.png) is defined
to be the set of all
is defined
to be the set of all 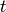 such that
such that 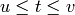 . One
might try to implement this as follows:
. One
might try to implement this as follows:
sage: W = WeylGroup("A2",prefix="s")
sage: [s1,s2] = W.simple_reflections()
sage: def bi(u,v) : return [t for t in W if u.bruhat_le(t) and t.bruhat_le(v)]
....:
sage: bi(s1,s1*s2*s1)
[s1, s1*s2, s1*s2*s1, s2*s1]
This would not be a good definition since it would fail
if 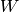 is affine and be inefficient of
is affine and be inefficient of 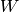 is large. Sage
has a Bruhat interval method:
is large. Sage
has a Bruhat interval method:
sage: W.bruhat_interval(s1,s1*s2*s1)
[s1*s2*s1, s2*s1, s1*s2, s1]
This works even for affine Weyl groups.
References:
The Bruhat Graph is a structure on the Bruhat interval.
Suppose that 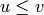 . The vertices of the graph are
. The vertices of the graph are
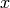 with
with 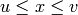 . There is a vertex connecting
. There is a vertex connecting
![x,y\in[x,y]](_images/math/6754c8992dbd3ab94fcdbc0752fa197bd94826c2.png) if
if 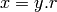 where
where  is a reflection.
If this is true then either
is a reflection.
If this is true then either 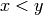 or
or 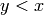 .
.
If 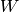 is a classical Weyl group the Bruhat graph is
implemented in Sage:
is a classical Weyl group the Bruhat graph is
implemented in Sage:
sage: W = WeylGroup("A3",prefix="s")
sage: [s1,s2,s3]=W.simple_reflections()
sage: bg=W.bruhat_graph(s2,s2*s1*s3*s2); bg
Digraph on 10 vertices
sage: bg.show3d()
The Bruhat graph has interesting regularity properties
that were investigated by Carrell and Peterson. It is
a regular graph if both the Kazhdan Lusztig polynomials
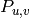 and
and 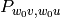 are 1, where
are 1, where 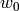 is the
long Weyl group element. It is closely related to the
Deodhar conjecture which was proved by Deodhar,
Carrell and Peterson, Dyer and Polo.
is the
long Weyl group element. It is closely related to the
Deodhar conjecture which was proved by Deodhar,
Carrell and Peterson, Dyer and Polo.
Deodhar proved that if 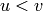 then the Bruhat interval
then the Bruhat interval
![[u,v]](_images/math/9efeb253b42a2c23e3861fab7e820e757e386961.png) contains as many elements of odd length as it
does of even length. We observe that often this can be
strengthened: if there exists a reflection
contains as many elements of odd length as it
does of even length. We observe that often this can be
strengthened: if there exists a reflection  such
that left (or right) multiplication by
such
that left (or right) multiplication by  takes the
Bruhat interval
takes the
Bruhat interval ![[u,v]](_images/math/9efeb253b42a2c23e3861fab7e820e757e386961.png) to itself, then this gives
an explicit bijection between the elements of odd and
even length in
to itself, then this gives
an explicit bijection between the elements of odd and
even length in ![[u,v]](_images/math/9efeb253b42a2c23e3861fab7e820e757e386961.png) .
.
Let us search for such reflections. Put the following commands in a file and load or attach the file:
W = WeylGroup("A3",prefix="s")
[s1,s2,s3]=W.simple_reflections()
ref = W.reflections().keys()
def find_reflection(u,v):
bi = W.bruhat_interval(u,v)
ret = []
for r in ref:
if all( r*x in bi for x in bi):
ret.append(r)
return ret
Now inspect the output of this command:
sage: for v in W:
....: for u in W.bruhat_interval(1,v):
....: if u != v:
....: print u,v,find_reflection(u,v)
This shows that the Bruhat interval is stabilized by
a reflection for all pairs 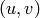 with
with 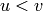 except
the following two:
except
the following two: 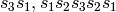 and
and
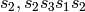 . Now these are precisely the pairs
such that
. Now these are precisely the pairs
such that 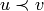 in the notation of Kazhdan and
Lusztig, and
in the notation of Kazhdan and
Lusztig, and 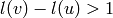 . One should not rashly
suppose that this is a general characterization of
the pairs
. One should not rashly
suppose that this is a general characterization of
the pairs 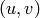 such that no reflection stabilizes
the Bruhat interval, for this is not true, but it does
suggest that the question is worthy of further
investigation.
such that no reflection stabilizes
the Bruhat interval, for this is not true, but it does
suggest that the question is worthy of further
investigation.