The Iwahori Hecke algebra is defined in:
Nagayoshi Iwahori, On the structure of a Hecke ring of a Chevalley group over a finite field. J. Fac. Sci. Univ. Tokyo Sect. I 10 1964 215–236 (1964).
In this original paper, the algebra occurs as the convolution ring of functions on a p-adic group that are compactly supported and invariant both left and right by the Iwahori subgroup. However Iwahori determined its structure in terms of generators and relations, and it turns out to be a deformation of the group algebra of the affine Weyl group.
Once the presentation is found, the Iwahori Hecke algebra can be
defined for any Coxeter group. It depends on a parameter 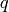 which in Iwahori’s paper is the cardinality of the residue field.
But it could just as easily be an indeterminate.
which in Iwahori’s paper is the cardinality of the residue field.
But it could just as easily be an indeterminate.
Then the Iwahori Hecke algebra has the following description.
Let 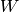 be a Coxeter group, with generators (simple reflections)
be a Coxeter group, with generators (simple reflections)
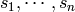 . They satisfy the relations
. They satisfy the relations 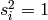 and
the braid relations
and
the braid relations
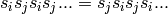
where the number of terms on each side is the order
of 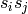 .
.
The Iwahori Hecke algebra has a basis 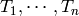 subject to relations that resemble those of the
subject to relations that resemble those of the 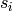 .
They satisfy the braid relations and the quadratic
relation
.
They satisfy the braid relations and the quadratic
relation
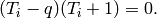
This can be modified by letting 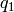 and
and 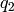 be two
indeterminates and letting
be two
indeterminates and letting
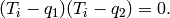
In this generality, Iwahori Hecke algebras have significance far beyond their origin in the representation theory of p-adic groups. For example, they appear in the geometry of Schubert varieties, where they are used in the definition of the Kazhdan-Lusztig polynomials. They appear in connection with quantum groups, and in Jones’s original paper on the Jones polynomial.
Here is how to create an Iwahori Hecke algebra:
sage: R.<q>=PolynomialRing(ZZ)
sage: H=IwahoriHeckeAlgebraT("B3",q); H
The Iwahori Hecke Algebra of Type B3 in q,-1 over Univariate
Polynomial Ring in q over Integer Ring and prefix T
sage: T1,T2,T3 = H.algebra_generators()
sage: T1*T1
(q-1)*T1 + q
If the Cartan type is affine, the generators will be numbered starting with T0 instead of T1.
You may coerce a Weyl group element into the Iwahori Hecke algebra:
sage: W = WeylGroup("G2",prefix="s")
sage: [s1,s2]=W.simple_reflections()
sage: P.<q>=LaurentPolynomialRing(QQ)
sage: H = IwahoriHeckeAlgebraT(W,q)
sage: H(s1*s2)
T1*T2
The Iwahori Hecke operator can be used to study representations of p-adic groups that have fixed vectors with respect to the Iwahori subgroup. References:
- Rogawski, On modules over the Hecke algebra of a
-adic group, Invent. Math., Inventiones Mathematicae, 79, 1985, 3, 443–465,
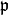 -adic groups. I. The
spherical function, Compositio Math., Compositio Mathematica, 40, 1980, 3,
387–406.
-adic groups. I. The
spherical function, Compositio Math., Compositio Mathematica, 40, 1980, 3,
387–406.A key feature of the theory are the intertwining operators between different induced representations. We will show how to implement these intertwining operators in Sage.
For simplicity we will work over 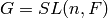 where
where 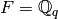 ,
with
,
with 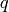 a prime number, but everything works for an arbitrary split reductive group over a
nonarchimedean local field. If
a prime number, but everything works for an arbitrary split reductive group over a
nonarchimedean local field. If 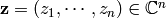 ,
define the following quasicharacters of
,
define the following quasicharacters of 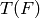 , the diagonal subgroup
in
, the diagonal subgroup
in 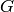 :
:
We extend both to characters of the Borel subgroup 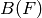 of upper triangular
matrices by letting the subgroup
of upper triangular
matrices by letting the subgroup 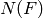 of upper triangular unipotent matrices
be in the kernels. Let
of upper triangular unipotent matrices
be in the kernels. Let 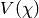 with
with 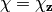 is defined to be
the space of locally constant functions
is defined to be
the space of locally constant functions 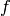 on
on 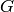 such that:
such that:
We have a representation 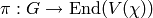 by right translation:
by right translation:
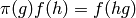 . These are the spherical principal series representations.
Let
. These are the spherical principal series representations.
Let 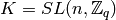 . This is the standard maximal compact subgroup. It has a
homomorphism
. This is the standard maximal compact subgroup. It has a
homomorphism 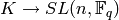 by reduction modulo
by reduction modulo 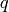 . The subgroup
. The subgroup 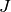 of elements of
of elements of 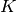 whose images are upper triangular is an open subgroup, the
Iwahori subgroup.
whose images are upper triangular is an open subgroup, the
Iwahori subgroup.
Suppose that the 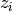 are all distinct. Then for each
are all distinct. Then for each 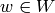 there exists
an intertwining integral
there exists
an intertwining integral 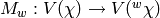 where the Weyl group
acts on characters of
where the Weyl group
acts on characters of 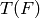 by conjugation. This integral is defined by the
formula
by conjugation. This integral is defined by the
formula
where 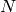 is the group of upper triangular unipotent matrices and
is the group of upper triangular unipotent matrices and 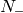 is the
group of lower triangular matrices. The integral is convergent provided
is the
group of lower triangular matrices. The integral is convergent provided 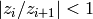 and in general it may be defined by analytic continuation in the
and in general it may be defined by analytic continuation in the  or another method.
See Casselman loc. cit..
or another method.
See Casselman loc. cit..
The problem is how to model the intertwining operators in Sage.
Let 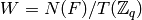 and
and 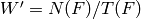 . These are isomorphic
to the affine and finite Weyl groups, that is, the Weyl groups with
Cartan types [`A`,n-1,1] and [`A`,n-1], respectively.
. These are isomorphic
to the affine and finite Weyl groups, that is, the Weyl groups with
Cartan types [`A`,n-1,1] and [`A`,n-1], respectively.
The Iwahori Hecke algebra 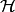 is the ring of compactly supported functions
is the ring of compactly supported functions 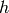 on
on 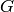 such that
such that 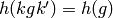 when
when 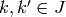 . It is a ring under convolution.
. It is a ring under convolution.
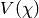 becomes a module over it by
becomes a module over it by
.
The subspace 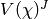 of
of 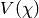 consisting of elements that are fixed by
consisting of elements that are fixed by
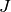 is invariant under
is invariant under 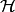 . This module is finite-dimensional: in
fact, its order is
. This module is finite-dimensional: in
fact, its order is 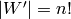 , whereas
, whereas 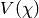 itself is infinite dimensional.
However the finite-dimensional
itself is infinite dimensional.
However the finite-dimensional 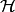 -module
-module 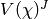 accurately reflects the
structure of the
accurately reflects the
structure of the 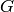 -module
-module 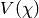 . For example
. For example 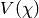 is irreducible
as a
is irreducible
as a 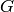 -module if and only if
-module if and only if 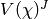 is irreducible as an
is irreducible as an 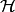 -module.
-module.
Normalizing the Haar measure so that 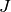 has volume
has volume 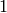 , let
, let 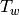 be the
characteristic function of
be the
characteristic function of 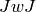 , and if
, and if 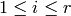 let
let
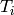 denote
denote 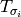 . The
. The 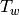 with
with 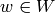 form a
basis, and the
form a
basis, and the 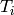 form a set of algebra generators The
form a set of algebra generators The 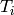 satisfy the
same braid relations as the
satisfy the
same braid relations as the 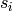 , but the relation
, but the relation 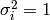 is
replaced by
is
replaced by 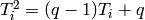 .
.
The subalgebra elements of 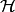 consisting of functions that are
supported in
consisting of functions that are
supported in 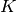 is the finite Iwahori Hecke algebra
is the finite Iwahori Hecke algebra 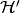 . Thus
. Thus
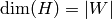 but
but 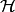 is infinite-dimensional The subalgebra
is infinite-dimensional The subalgebra 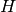 has generators
has generators 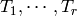 but omits
but omits 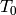 .
.
We see that 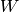 ,
, 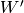 ,
, 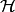 and
and 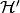 are all objects that
can be created in Sage.
are all objects that
can be created in Sage.
We define a vector space isomorphism 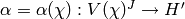 as follows. If
as follows. If 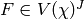 then let
then let 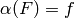 where
where 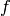 is the function
is the function 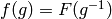 if
if 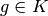 , 0 if
, 0 if 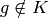 .
It may be checked that
.
It may be checked that 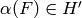 . This allows us to model the
. This allows us to model the 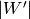 -dimensional
-dimensional
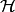 -module
-module 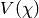 by the
by the 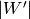 -dimensional subalgebra
-dimensional subalgebra 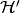 .
This idea, which appears in the paper of Rogawski cited above, is due to Joseph
Bernstein.
.
This idea, which appears in the paper of Rogawski cited above, is due to Joseph
Bernstein.
Let 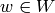 and define a map
and define a map 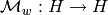 by requiring that
by requiring that
as maps from 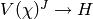 . Since
. Since 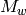 and
and 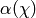 ,
,
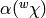 are all homomorphisms of left
are all homomorphisms of left 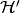 -modules,
-modules,
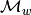 is a homomorphism of left
is a homomorphism of left 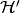 modules. Now let
modules. Now let
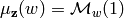 where
where 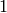 denotes the identity element
of
denotes the identity element
of 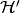 .
.
Because 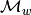 is a
is a 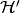 -module homomorphism, we have
-module homomorphism, we have
.
In other words, the intertwining operator is modeled by multiplication
by 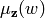 when we identify
when we identify 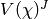 and
and 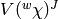 with
with
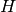 by means of the homomorphisms
by means of the homomorphisms 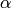 . We are therefore left with the
problem of computing
. We are therefore left with the
problem of computing 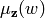 . If
. If 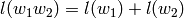 then
then 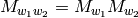 and it follows that
and it follows that
.
(Here 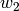 acts on the spectral parameters
acts on the spectral parameters  in the
obvious way.) Thus we are reduced to the determination of
in the
obvious way.) Thus we are reduced to the determination of 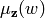 when
when 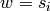 is a simple reflection, and this is accomplished by Theorem 3.4
in Casselman, loc. cit.:
is a simple reflection, and this is accomplished by Theorem 3.4
in Casselman, loc. cit.:
Here the simple root 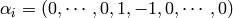 in the ambient lattice,
where the
in the ambient lattice,
where the 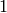 is in the
is in the 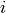 -th position, so
-th position, so 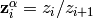 .
.
In addition to the intertwining operators, let us construct a basis 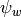 of
of
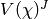 indexed by elements of
indexed by elements of 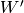 . Let
. Let
where 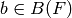 and
and 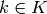 . In order to make sense of this definition,
bear in mind that every element of
. In order to make sense of this definition,
bear in mind that every element of 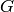 has a decomposition as a product
has a decomposition as a product 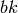 with
with
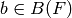 and
and 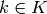 , and every
, and every 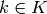 belongs to a unique double coset
belongs to a unique double coset
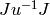 with
with 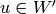 .
.
The image of 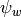 under the homomorphism
under the homomorphism 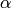 is just
is just 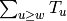 ,
and by abuse of notation we will denote this element of
,
and by abuse of notation we will denote this element of 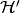 also
by
also
by 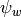 . Now let us ask to evaluate
. Now let us ask to evaluate 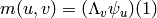 . It
may be shown that
. It
may be shown that 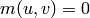 unless
unless 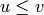 , and that
, and that 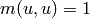 . In other
words, the “matrix”
. In other
words, the “matrix” 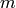 is upper triangular in the Bruhat order.
is upper triangular in the Bruhat order.
Bump and Nakasuji used Sage to investigate this question and arrived at the
following conjecture. This is conjectured for more general groups than just
the 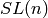 that we are considering, but only for the simply-laced groups
(types A,D,E). It follows from the Deodhar conjecture that the set
that we are considering, but only for the simply-laced groups
(types A,D,E). It follows from the Deodhar conjecture that the set
has cardinality 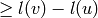 , where
, where 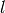 is the length function on
is the length function on 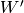 .
(Remember that
.
(Remember that 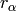 is the reflection in the positive root
is the reflection in the positive root 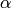 .)
If the Kazhdan-Lusztig polynomial
.)
If the Kazhdan-Lusztig polynomial 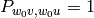 , then
, then
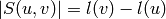 .
.
Conjecture (Bump and Nakasuji) If the Kazhdan-Lusztig polynomial 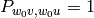 then
then
The following Sage code is capable of verifying this statement for ['A',3], and of course can be adapted to any root system.
This program can compute both the actual and conjectured values of 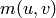 .
.
import copy
P1.<q>=PolynomialRing(QQ)
W = WeylGroup("A3",prefix="s")
KL = KazhdanLusztigPolynomial(W,q)
P.<q,z1,z2,z3,z4>=PolynomialRing(QQ)
F = Frac(P)
H = IwahoriHeckeAlgebraT(W,q,base_ring=F)
[s1,s2,s3]=W.simple_reflections()
w0 = W.long_element()
[T1,T2,T3]=H.algebra_generators()
def mu(z,s):
"""
Produces an element of the Hecke algebra that mimics
the intertwining integral corresponding to a simple
reflection.
"""
[z1,z2,z3,z4] = z
if s == s1:
return q^(-1)*T1+(1-1/q)*(z1/(z2-z1))
elif s == s2:
return q^(-1)*T2+(1-1/q)*(z2/(z3-z2))
elif s == s3:
return q^(-1)*T3+(1-1/q)*(z3/(z4-z3))
def reflect(s,z):
"""
Applies the simple reflection s to the spectral data z.
"""
return (Matrix(z)*s.matrix()).list()
def intertwiner(w,debug=False):
"""
This is mu_z(w) in general. The function mu(z,s) implemented
above is only for simple reflections.
Run with debug=True to see what it is really doing.
"""
decomp = w.reduced_word()
decomp.reverse()
prod = H(1)
if debug:
clist = ""
for i in range(len(decomp)):
alist = copy.deepcopy(decomp[:i])
z = [z1,z2,z3,z4]
for j in alist:
z = reflect(W.simple_reflection(j),z)
s = W.simple_reflection(decomp[i])
if debug:
clist +="mu(%s,%s)"%(z.__repr__(),s.__repr__())
if i < len(decomp)-1:
clist += "*"
else:
prod = prod*mu(z,s)
if debug:
return clist
else:
return prod
def psi(u):
"""
u is a permutation. This produces the sum of the f_v for v>=u.
"""
u = H(u).support_of_term()
return sum(H(v) for v in W if u.bruhat_le(v))
def ev(f):
"""
Evaluate the element of the space of Iwahori fixed vectors
in the induced model at the identity.
"""
return f.coefficient(W(1))
def m(u,v):
"""
It is assumed that u <= v. Apply the v intertwiner to
psi(u) and evaluate at 1.
"""
u = W(u)
v = W(v)
return ev(psi(u)*intertwiner(H(v)))
def rfactor(alpha):
"""
If alpha is a root, returns (1-q^(-1)*z^alpha)/(1-z^alpha).
"""
z = [z1,z2,z3,z4]
za = prod(z[i]**alpha[i] for i in range(4))
return (1-q^(-1)*za)/(1-za)
def conjectured_m(u,v):
"""
This is the value conjectured for m(u,v) by Bump and Nakasuji
if u and v satisfy a hypothesis.
"""
refdict = W.reflections()
S = [refdict[r] for r in refdict.keys() if u.bruhat_le(v*r) and (v*r).bruhat_le(v)]
return prod(rfactor(alpha) for alpha in S)