Characters of Abelian Groups

Now let $G$ be a finite abelian group, which we will write multiplicatively. Let $L^2 (G)$ be the inner product space of all complex-valued functions on $G$, with the inner product \[ \left\langle \phi, \psi \right\rangle = \frac{1}{|G|} \sum_{g \in G} \phi (g) \overline{\psi (g)} . \] It is a finite-dimensional Hilbert space.

By a linear character $\chi$ of $G$, we mean a homomorphism $\chi : G \longrightarrow \mathbb{C}^{\times}$. The linear characters form an abelian group under multiplication, which we will denote $G^{\ast}$. If $n$ is a positive integer, we will denote by $\mu_n$ the group of $n$-th roots of unity in $\mathbb{C}$.

Lemma 2.2.1: If $\chi$ is a linear character of the finite group $G$, then $| \chi (g) | = 1$ for all $g \in G$. In fact, if $\chi (G) \subset \mu_n$, the group of $n$-th roots of unity in $\mathbb{C}$, where $n$ is the exponent of $G$.

Proof. (Click to Expand/Collapse)

It is trivial that if $g \in G$ then $g^n = 1$, and so $\chi (g)^n = 1$, and so $\chi (g) \in \mu_n$. Of course this implies $| \chi (g) | = 1$ in $\mathbb{C}$.

Lemma 2.2.2: If $\chi, \theta \in G^{\ast}$, then \[ \left\langle \chi, \theta \right\rangle = \left\{ \begin{array}{ll} 1 & \text{if $\chi = \theta,$}\\ 0 & \text{otherwise} . \end{array} \right. \]

Proof. (Click to Expand/Collapse)

If $\chi \neq \theta$ then $\chi (x) \neq \theta (x)$ for some $x \in G$. Since $| \theta (g) | = 1$, $\overline{\theta (g)} = \theta (g)^{- 1}$ for all $g \in G$. Now \[ \left\langle \chi, \theta \right\rangle = \frac{1}{|G|} \sum_{g \in G} \chi (g) \overline{\theta (g)} = \frac{1}{|G|} \sum_{g \in G} \chi (g) \theta (g)^{- 1} . \] Now we permute the elements of $G$ by making the substitution $g \longmapsto g x$ and obtain \[ \left\langle \chi, \theta \right\rangle = \frac{1}{|G|} \sum_{g \in G} \chi (x g) \theta (x\,g)^{- 1} = \chi (x) \theta (x)^{- 1} \frac{1}{|G|} \sum_{g \in G} \chi (x g) \theta (x\,g)^{- 1} = \chi (x) \theta (x)^{- 1} \left\langle \chi, \theta \right\rangle . \] Since $\chi (x) \neq \theta (x)$, this implies that $\left\langle \chi, \theta \right\rangle = 0$.

On the other hand if $\chi = \theta$ then $\chi (g) = \theta (g)$ for all $g$, so \[ \left\langle \chi, \theta \right\rangle = \frac{1}{|G|} \sum_{g \in G} \chi (g) \theta (g)^{- 1} = \frac{1}{|G|} \sum_{g \in G} 1 = 1. \]

We see that the linear characters of $G$ are orthonormal. We will eventually show that they are an orthonormal basis of $L^2 (G)$, but we need some further preparations before we can show this.

Lemma 2.2.3: If $G$ is finite abelian group and $H$ a proper subgroup, and if $\chi$ is a linear character of $H$, then $\chi$ can be extended to a subgroup of $G$ that is larger than $H$.

To say that $\chi$ can be extended to a subgroup $K$ of $G$ that contains $H$ means that we can find a linear character $\tilde{\chi}$ of $K$ such that $\tilde{\chi} (h) = \chi (h)$ when $h \in H$.

Proof. (Click to Expand/Collapse)

Let $x \in G - H$. There is a smallest positive integer $d$ such that $x^d \in H$. Then $x^n \in H$ if and only if $n$ is a multiple of $d$. Find a complex number $a$ such that $a^d = \chi (x^d)$. Let $K = \left\langle H, x \right\rangle$. This is the subgroup of elements of $G$ that can be written in the form $x^n h$ for some $h \in H$. We claim that we can define a character $\tilde{\chi}$ of $K$ by $\tilde{\chi} (x^n h) = a^n \chi (h)$.

We must check that this is well defined. If $x^n h = x^m h'$, then $h' h^{- 1} = x^{n - m}$, so $n - m$ is a multiple of $d$, say $n - m = d k$. Then \[ \chi (h') \chi (h)^{- 1} = \chi (x^{n - m}) = \chi (x^d)^k = a^{d k} = a^{n - m}, \] which implies that $a^n \chi (h) = a^m \chi (h')$. Thus $\tilde{\chi}$ is well-defined. It is easily seen to be a homomorphism, that is, a linear character.

Proposition 2.2.1: Let $G$ be a finite abelian group, and let $H$ be a subgroup of $G$. Let $\chi$ be a linear character of $H$. Then $\chi$ can be extended to a linear character of $G$.

Proof. (Click to Expand/Collapse)

Let $\Sigma$ be the set of subgroups $K$ of $G$ such that $K \supseteq H$ and $\chi$ can be extended to $K$. The set $\Sigma$ is nonempty since $H \in \Sigma$, so let $K$ be a maximal element. If $K$ is a proper subgroup of $G$, then an extension of $\chi$ to $K$ exists but cannot be extended to any larger subgroup, which contradicts Lemma 2.2.3. Thus $K = G$.

Proposition 2.2.2: Let $G$ be a finite abelian group, and let $x, y \in G$. If $\chi (x) = \chi (y)$ for all $\chi \in G^{\ast}$, then $x = y$.

Proof. (Click to Expand/Collapse)

Let $z = x y^{- 1}$ have order $n$. We can define a linear character of $\left\langle z \right\rangle$ by $\chi (z^k) = e^{2 \pi i k / n}$. If $z \neq 1$ then $\chi (z) \neq 1$, and extending $\chi$ to a character of $G$ by Proposition 2.2.1 gives a contradiction. So $z = 1$ and $x = y$.

Let $G$ be a finite abelian group, and let $x \in G$. Then $x$ determines a function $\check{x}$ on $G^{\ast}$, namely the map $\check{x} (\chi) = \chi (x)$. The fact that $x$ is determined by $\check{x}$ is a consequence of Proposition 2.2.2.

Proposition 2.2.3: Let $G$ be a finite abelian group.

(i) We have $|G| = |G^{\ast} |$.

(ii) If $x \in G$, then $\check{x} \in (G^{\ast})^{\ast}$, and the map $x \longmapsto \check{x}$ is an isomorphism $G \longrightarrow (G^{\ast})^{\ast}$.

Proof. (Click to Expand/Collapse)

We have $\check{x} (\chi \chi') = \chi \chi' (x) = \chi (x) \chi' (x) = \check{x} (\chi) \check{x} (\chi')$, so $\check{x}$ is a character of $G^{\ast}$. To see that $x \longmapsto \check{x}$ is a homomorphism, observe that \[ \check{x} \check{y} (\chi) = \check{x} (\chi) \check{y} (\chi) = \chi (x) \chi (y) = \chi (x y) = \check{(x y)} (\chi), \] because $\chi$ is a character. We see that $x \longmapsto \check{x}$ is a homomorphism $G \longrightarrow (G^{\ast})^{\ast}$.

We can now prove (i) and (ii) simultaneously. We first observe that $|G^{\ast} | \le |G|$ since the linear characters are an orthonormal set, hence linearly independent. Applying this twice, $| (G^{\ast})^{\ast} | \le |G|$. But $x \longmapsto \check{x}$ is a homomorphism $G \longrightarrow (G^{\ast})^{\ast}$ that is injective by Proposition 2.2.2. We see that $|G| = | (G^{\ast})^{\ast} |$ and $x \longmapsto \check{x}$ is an isomorphism. Now $|G| = | (G^{\ast})^{\ast} | \le |G^{\ast} |$ and so $|G| = |G^{\ast} |$.

Because $x \longmapsto \check{x}$ is an isomorphism, we may identify $x$ with $\check{x}$ and regard elements of $G$ as characters of $G^{\ast}$. This means that the roles of $G$ and $G^{\ast}$ are symmetrical.

Theorem 2.2.1: Let $G$ be a finite abelian group. Then $G^{\ast}$ is an orthonormal basis of $L^2 (G)$.

Proof. (Click to Expand/Collapse)

We have already shown that $G^{\ast}$ is an orthonormal set, hence linearly independent. But $|G^{\ast} | = |G| = \dim (L^2 (G))$, and so they are a basis.

Exercise 2.2.1: If $G$ and $H$ are finite abelian groups, prove that \[ (G \times H)^{\ast} \cong G^{\ast} \times H^{\ast} . \]

Exercise 2.2.2: If $G$ is a finite abelian group, prove that $G \cong G^{\ast}$. (Hint: reduce to the case of a cyclic group.)

Exercise 2.2.3: (Fourier inversion formula.) Let $\mathcal{F}: L^2 (G) \longrightarrow L^2 (G^{\ast})$ be the Fourier transform, defined by $\mathcal{F}f = \hat{f}$, where $\hat{f}$ is the function on $L^2 (G^{\ast})$ defined by \[ \hat{f} (\chi) = \frac{1}{\sqrt{|G|}} \sum_{x \in G} \chi (x) f (x) . \] Prove that \[ f (g) = \frac{1}{\sqrt{|G|}} \sum_{x \in G} \overline{\check{x} (\chi)} \hat{f} (x) . \]

Exercise 2.2.4: (Plancherel formula.) Prove that $\mathcal{F}$ is an isometry, that is $\left\langle f_1, f_2 \right\rangle = \left\langle \widehat{f_1}, \widehat{f_2} \right\rangle$.

Although Exercise 2.3 shows that $G \cong G^{\ast}$, this is a less natural isomorphism than the isomorphism $G \cong (G^{\ast})^{\ast}$. The isomorphism $G \longrightarrow (G^{\ast})^{\ast}$ was defined in a canonical way, but any description of the isomorphism $G \cong G^{\ast}$ will depend on arbitrary choices. For example, if you solve Exercise 2.2.2 by first decomposing $G$ as a direct product of cyclic groups, the proof will depend on the choice of this decomposition.

The operation $^{\ast}$ is actually a functor, which means that it is not only an operation on abelian groups, but also on their homomorphisms. Indeed, if $f : G \longrightarrow H$ is a homomorphism of abelian groups, then there is induced a homomorphism $f^{\ast} : H^{\ast} \longrightarrow G^{\ast}$, which is composition with $f$. Thus if $\chi \in H^{\ast}$, then $\chi \circ f \in G^{\ast}$, and this is $f^{\ast} (\chi)$. Now the functor $\ast$ is contravariant since it reverses the direction of arrows. On the other hand, iterating it gives a covariant functor $\ast \ast$, since the direction of arrows is twice reversed: since $f^{\ast}$ is a map $H^{\ast} \longrightarrow G^{\ast}$, $(f^{\ast})^{\ast}$ is a map $(G^{\ast})^{\ast} \longrightarrow (H^{\ast})^{\ast}$. Now the naturality of the isomorphism $\check : G \longrightarrow (G^{\ast})^{\ast}$ can be expressed with the observation that the following diagram commutes:

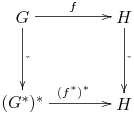
No such property exists for the contravariant functor $\ast$.

Yet another reason that the isomorphism $G \cong G^{\ast}$ should be regarded as less fundamental than the isomorphism $G \cong (G^{\ast})^{\ast}$ is that the whole theory can be generalized to the setting of topological groups. Specifically, let $G$ be a locally compact abelian group. This means first of all, that $G$ is a Hausdorff topological group (so that it is a Hausdorff topological space, and the group operations are continuous) and that every point has a neighborhood whose closure is compact; and that $G$ is abelian. In this setting, everything we have done except Exercise 2.3 goes through without essential change. The characters $\chi : G \longrightarrow \mathbb{C}^{\times}$ are required to be continuous and unitary, which means that $| \chi (g) | = 1$. The character group $G^{\ast}$ is given the topology where a sequence converges if it converges uniformly on compact sets. We have $G \cong (G^{\ast})^{\ast}$ (Pontriagin duality) and the Fourier transform is an isometry $L^2 (G) \longrightarrow L^2 (G^{\ast})$. Fourier analysis was first carried out in the setting of locally compact abelian groups in a monograph of André Weil.

However $G$ and $G^{\ast}$ may or may not be isomorphic. We have seen that they are isomorphic of $G$ is finite; or if $G =\mathbb{R}$ (the additive group) or $\mathbb{Q}_p$ (the additive group of $p$-adic numbers) then $G \cong G^{\ast}$. But if $G =\mathbb{R}/\mathbb{Z}$ then $G^{\ast} =\mathbb{Z}$, and it is in this setting that most people first encounter Fourier analysis. A function $f$ on the circle $G =\mathbb{R}/\mathbb{Z}$ is transformed into a sequence of coefficients $\hat{f} (n)$ where \[ \hat{f} (n) = \int_0^1 f (x) e^{i n x} d x. \] The integer $n$ corresponds to the character $e^{i n x}$ of $\mathbb{R}/\mathbb{Z}$, and the Plancherel formula is the assertion that \[ \int_0^1 f (x) \overline{f' (x)} \, d x = \sum_n \hat{f} (n) \overline{\hat{f}' (n)} . \]